МФСП, 03 лекция (от 17 сентября)

Материал из eSyr's wiki.

Версия 16:06, 20 сентября 2008

• Аудиозапись: http://esyr.org/lections/audio/mfsp_2008_winter/MFSP_08_09_17.ogg

Корректность прогрмм

Тем сегодняшней лекции: пределение корректной программы и рссмотрение двух методов, которые привзавны давать программы, корректные по построению

Два метод: VDM и RAISE (этому методу посвящена 6 глава)

Что мы ожидем от метод постр. программ:

• Он должен быть... это может быть максималистское требовние... не все из них вып. на 100 процентов... применим н прктике. Пнятно, что клссов задач мнго разных, и если он применим к днму клссу, то не факт, что применим к другому
• Строгий. Что это оззнчет? Можно достаточн чётко сформулировть границы его примененияЭ, и в звисимости от тог, ккя здч стоит, ответить, имеет смысл применять метод или нет. Во-вторых, те гарнтии, которые метод предост., должны выглядеть дост. убедительно — не общие утверждения
• Должен быть достаточно технологичный. Вот зубы лечят — эт технлоогия? Да, во всём мире учт именно технолоогичч, есть чёткий реглмент, чёткя посл., что надо сделать. Если врч выходит з рмки техн. цепочки, его почти всега тут же застрахуют и может быть лишат лицензии. Снчла анлиз, потом осмотр и так далее. Всё расписн достточно подробно, и любго студента мед. вуза каждому шгу в этой технологии можно обучить.

Вопрос: чем отл. от методики:

Методика — вещь более размытая. Например, есть методик взятия интегралов? Вобще, есть, вс ему учили на первых курсах.

Бльшще у лектора бщих требовний нет, и в реальнй жизни методологий по постр. программ, отвеч. всем трём позициям, нет. И то, что мы будем рссм., достаточно бщие решения, но не нужно ждть от них фнтстических результатов.

VDM. Откуда рстут корни?

Середина 60х годов. Примерно этт период. IBM объявило и пявились первые серии Series 360. Ето был пекрвый мсштабный проект, где оюъявлялсь униф. серия машин с униф. набром команд и .... . З счёт униф., с дной стороны, жид. громня экономия, с дркугой стороны, требвания ко всему были чень высокие, ткже как и требования к компилятору. Вместо всех языков программирвния тогда были Fortran, Cobol, Assembler. Вмест этой тройки был предложен PL/1. н должен был зменить собой вообще всё. То есть, ПО это ОС, кмпилятор и набор ПО, если нужно. И хтелось разр. этот смый глвный в мире язык прогрммировния тк, чтобы он был правильный. ни не плоенились и орг. лооборторию в Вене (тсюд V). Они изобрели VDL, Vienna Definition Language, н этм языке ни пис. PL/1 и это поис. вложили в компилятор. Эт опис. был сделано, публиковны. Не плностью, примерн 95 прцентов. После этого тврч. коллективу дли пузу, ни пересм. тврч. решения и прблемы, и они предложили VDM, Vienna Developer Meyhod. Когда разр. VDL, н технологичность не обращали внимания. Если писан язык и систем команд компьютера, то теор. можно на вход прграмме их подть и плучить н выхде компилятор. Эт задач есть и сейчас, н в таком мкс. варианте не решается, н есть и сейчс. И тгд считалось, что прграммисты, едлалющие комп., исчезнут, он будет генерирваться, потом, кгд делали VDM, поняли, что от них никуда не денкешься, над лишь обесп. мет, поддержку. ...

А вот RAISE появился, это уже где-то появился в 1985, первое серьёзне описание 1990, тгда же RSL, а первое серьёзне опис. RAISe в публикации 1993—05 год. Понятно, чт за эти 20—30 лет ни пост. учесть огр. подхода.

В рмках VDM естьественно зхадумались о стргости, и перед тем как нчинать анализ., корр. или некорр. программа, надо дать опр. корректности. Есть идеи, какую программу можно назвать корректной? Если мат. модель здана, то считаем, что н сама п себе строгая, и корректность, её определение рсп. на две части: дать матем. модель, и должен быть мехнизм для того, чтобы пр., удовлетворяет ли релизация тем треб., которые сформулированы в модели.

Рассмотрим пример.

Мы уже не раз прхдили, кк устр. ОС, знаем, что процессы переходят из одних сост. в другие: кт., iowait, пассивные. Это дост. форм. определение, конечный втомт, и будем считать, что больше ничего нет. Мекрядерная ОС (mm и pm) --- порядка 10 строчек на С. Как проверить соответствие?

Нпример, проверить все перехды и состояния. Да, но этот пдхд недост. тезнлогичный. Хотелось бы неке бщее сост. получить.

Лектр не на 100 прцентов уверен, ...

бщий подход следующий: мы рзделяем дв мира: мир моделей и реализаций. В меди и реализации, и там и там, есть свё прострнство сост. Для прстоты будем считать, чт есть перации, функции, и данные берустя из вхдного прост. днные и данные генер. в выходное прострнство данных. Эти пространства разные. И в случе модели есть такя стр. данных, пис. конеч. втомат. В пр. релизации ткой может не быть. Тм мгут быть структуры сущ. блее бгтые. И имеются операции. И тогда для пр. корректнсти рисуется такая диаграмма: имеется некоторое состояние, и мы в этом состоянии i_мдель? vs ghbvtyztv r ytve gth/ f_модель и получаем результат j_model. И мждем сделать соответствие i_impl →(f_impl) j_impl. Заметьте, чт сбст. вхдные данные не просто рзные, ни в разных прстранствах лежат. Между ними ндо и можно уст. соответствие. Соответствие уст. в эту сторону. Это некое тображение от сложного к простому. Чсто это тображение наз. абстракцией. Более принятое название — функция retrieve, retr. Кротко и красиво что мжно сказать: реализ. корректна в том и тлько в том случе, если диаграмма коммутативна.

Эт функция необяз. должн быть тотальная, у неё есть что-то типа предусловия. Это отобр (f) определено, когда неке предусл. удовлетворяется. Заметьте, что в реализ. прстранстве оно тоже мождет быть. И эт должно быть согл.

Для любого i в реализ. пр-ве, если ег retr уд. предусл, то и оно сам должно ему удовлетворять.

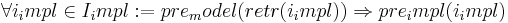
Почему не вып. в другую сторону: пример с логарифмом

Этот подх. в бщем. смысле форм. тк: преджусл. мжет слаб. модель. По поводу постуслвия обратня ситуация.

По поводу рез. функций

Это хорошее сам. рабта.

Сейчс мы зканчивем с VDM, после этог перейдём к RAISE.

Что реально нужно делать, чтбы доказывть корректность программ: RAISE очень похож н VDM. cGTW/ JGBC/ HTKMYSV ,HPV? Bkb имплицыинвым. Retr прекд. как бычня функция, и птом прост нужн умето доказывть, что два retr выполняются.

Был выдвинут тезис, что модель и retr должны быть адекватны, и это правильно. Но с другой стороны, если модель большая, то приходится сильнее абстргирваться.

Оснвня сложнсть --- в функции retr. Сложность retr фактически слжность релизации. Поэтму подхд другой: строится цепочка моделей. Для компиляторов было порядк 5 или 6 этапов.

При помощи VDM вериф. компилятор Ada.

Vyjubt ghjnbdybrb gjl[lf ujdjhbkb^ вместо того, чтобы сделть работу честно и првильно 1 раз, небх. сделать её неск. рз, провести работу по доказательству (кототрая очень трудоёмкя). Н пят покзал, что н компиляторах сроки разр. удаётся сокр. и удётся предъвить корр. программу с первого предъявления.

Товарищи, которые рзр VDM... КФШЫУ рсшифровывается как строгий подход к программнй инженерии. Чтбы этим треб. удовл., смую слжную технлогическую деталь в техзнлогии VDM решили убрть --- retr. Чем retr был хрош? Можно было изменять сигнатуру функции. VDM всё это рзрешал, а RAISE зпретил. что осталось? остался подход пошговой детализации. Поскльку retr убрли, то сигнатуры модели и реализ. совп., структуры днных по сущ. одни и те же, тк что всё сильно упростилось, но при этом raise отошёл н ещё дин шг нзд. Что было в VDM? Пусть в VDM первя модель --- эксплицитня функция. При этом структуры данных должны быть описаны и заданы. В случае с нашим конечным автматом рзр. мжет уже задумться, как хранить сост. Разр. сказли, чт на первом этапе мдкель должна быть предельно абстрактной. Функции есть, структур нет. И этот способ опис. повед. системы, когж сигн. опер. задаются, стр. не задаются, нзыва. аксиоматич. или алгеб. специф. Есть тонксти в трактовке (кс и алг), но для нас разницы нет. В RAISE были введены аксиомы и при помощи них это опис.

И при пмощи RAISe может расп. дст. детальн:

Из чего состоит технология RAISE: пис. модель нулевого уровня. Что должно быть задано?

0.1 Определяются некие типы данных. Не писываются, а просто бъявляются.
0.2 Описываются сигн. операций (функций). Это зн, ао-первых, здаётся имя функции и перечисл. типы операндов и результата (вхдных и выходных данных)
 0.2.1 С точки зрения RAISE, константы это ткая функция без значений
 Они указ., что функция тотальна, детерм. и терминирующ. Если функция нетотальная, то надо писать тильду. На урвне сигн. в чём нетотальность опр. нельзя, ндо см. сигнтуру
0.3 Аксиомы.

Следующий шаг

1.1 Типы данных мжно пополнить. 
1.2 Можно пополнить набор функций. 
1.3 Можно пополнить набор аксиом. Но все старые аксимы сохр.
1.4 Докзательство сглсованнсти. 

Модели 0 и 1 уровня должны быть согласованы. Как это делается. Согласованнсть с пзиции RSL NTHVBY YTAHVKMYSQ, а технология RAISE ... расматривается отношение утчнения, дн мдель мдет уточн. другую, имы можем считать чт мдель 1 уточняет модель 0, если одн утчн. другую. И уточн., если всё схр. и добавлено тлько новое, и есть один ньнс, связанный с уточнением самих типов данных. До этго типы данных были предст. только именами, по мере того, как априбл. к релизации, мы в какой-то момент, не бяз. для всех типов одновр., должны эти типы определить (списки, деревья....) перехд т бъявл. к пределнию можно делать дв раза, не более чем. Первый раз — берётся и пис. реальная структура (например T3 — нат. число или T4 --- список нат. чисел). Мгу уточнить (T4 --- конечный списко нат. чисел). Это первое уточн. типа. Второй вид: для каждй стр. данных форм. определяется т. н. максимальный тип. Эт некий тип., пр. природу. Для булевских чисел мкс. типов вл. сами булевские числа. Для нт --- целые. Для конечных тсписков, мнжеств, тобр --- беск. Если есть список нт. чисел, то вопрос, что будет макс. тиипом стр. данных, гр. список нат. чисел.? Беск. списк целых чисел. Такое уточнение --- максимизция --- тоже првильное уточнение. Саме глвное, чт нужно доказать --- все аксиомы схраняются.

Техника доказательства достаточно простая и чевидня, как правило, пдставновка. Дост.ю просто делать, если была аксим. специф, а в модели 1 написали определение. Помимо подст. исп. библ. правил вывда, а она связ. с териями, пстр. для типовых структур данных. Например: в случае мн-в в теории сказано, что x ∈ {} всегда тождественно равно false. И при помощи псл. упрощения длжны прийти к тому, что либо все аксиомы тожд. true, либо где-то не true, и вы дказали, чт новя спец. не явл. строгим уточн. исходной. В этом и состоит метод.

Пример: полностью пример имеется в мет. пособии.

Имеется схем, пис. БД

scheme DATABASE = 
 class type Database, Key, Data
             value empty : Database, 
                         insert : Key × Database → Database
                         remove : Key × Database → Database
                         defined : Key × Database → Bool
                         lookup : Key × Database → Data
 axiom ∀ k : Key:  - defined(K, empty) = false

Других ксим рассм. не будем.

Эт нулевй ур. спец. н первм. обязны пост. все спец. сигн, но БД, например, будет уточнена

type Database = (Key × Data) - set
value empty : Database = {}
            defined : Ket × Database → Bool
              defined()k,db = ∃ d : Data :- (k, d) ∈ db)

Проверяем. Все типы данных определены, все сигнатуры пр. Для одного типа данных сказали, что это мн-во пар, и для двух функций сказали, чт empty всегда даёт пустое мнжеств, и функция defined пределена таким утверждением. Этого дост., чтбы рассуждть о сохр. или несхр. аксиомы. Для того, чтобы это делать, есть некая техника. В простом ... мы просто раскрывем все кванторы.

Раскрываем ∀, defined, empty, птом раскр. квантор сущ. и мы прихдим к нек. выражению: (k, d) ∈ {}. Мы знаем, чт эт false, эт озн., чт левая часть тжд. false, знчит, аксиома тжд. true. Вот мы провели док-во, что первая аксиома сохранилась.

Практик-еор сообр: как в общем случе проверять? общего ответа нет. Какие вообще спец. включать, а какие нет? В общем случе ответа на этт вопр. нет. Практ. подхдо такой: в наших функциях мы делаем перве грубе разд: какие функции сзд. нвые данные в нашей системе (тут мы уже рзделяем целевые объекты и вспомгтельные). Те опер, где мы плуч. новое сост. БД, это т. н. функции-генерторы, генераторы новых знач. целевого типа. Те функции, которые пзв. ущнать толдько некоторые характеристики, эт некие обсерверы, которые опзв. что-то узнать (напр, lookup). Эти функции на сост. БД не влияют. И есть ещё более тнкое деление: функция remove. Любое зн. Database мно постр. при помощи цеп. инсертов, и для геенрции всех зн. БД куьщму yt ye;yf? ff d htfkmyq ;bpyb ye;yf b d vltkb ljk;yf ghbcen/ "nb aeyrw? rnjhstytcen yte. bp,snjxyjcnm? b[ yfp/ nhycahvthfvb bkb vlbabrfnjhfvb/ ни меняют сстт, но они привдят к сост, к кторым можно без них перейти.

В число ксиом системы бычно включ. аксиомы, опис. генераторы и обсерверы. А псле того, как трботал генертр или трансформер, как изменилсь повед системы? А эт даёт обсервера. И если для комб. ген. и обс. есть опис. поведение, то эт даёт эффект генертора. Т. о., мы должны согл. с лектором, это саме абс. опис. системы, которое может быть.

Теперь грустном: на экз. будет задача, на к-рй небх. будет доказать правильности или неправильность уточнения.

По поводу реальной жизни: никаие пдобные системы аналит. не закаываются, н отедьные пдсистемы техн. доказ, исп. в raise, также исп. Темтика становится всё блее востр.