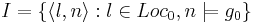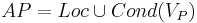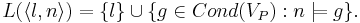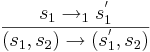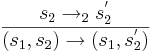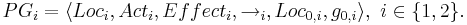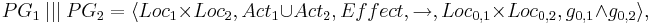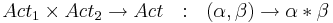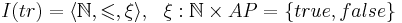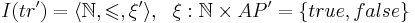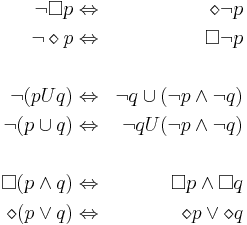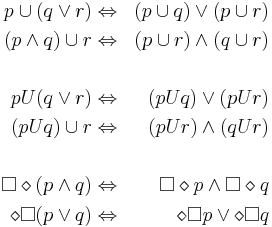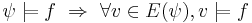ВПнМ/Теормин
Материал из eSyr's wiki.
(/* Подходы к верификации программ. Верификация программ на моделях. Процесс верификации программы при помощи её модели. Область применен) |
(Отмена правки № 11255 участника 95.159.154.71 (обсуждение)) |
||
| (187 промежуточных версий не показаны.) | |||
| Строка 1: | Строка 1: | ||
== Моделирование и абстракция == | == Моделирование и абстракция == | ||
=== Моделирование программ. Понятие состояния. Потенциальные и достижимые состояния. Требования к модели. Процесс построения модели. === | === Моделирование программ. Понятие состояния. Потенциальные и достижимые состояния. Требования к модели. Процесс построения модели. === | ||
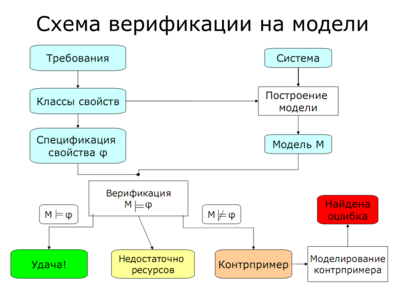
| - | Схема верификации на моделях (Лекция 2, слайд 3) | + | [[Изображение:Verif1.png|400px|thumb|right|Схема верификации на моделях (''Лекция 2, слайд 3'')]] |
| - | '''Состояние программы''' - совокупность значений | + | '''Состояние программы''' - совокупность значений объектов данных и счётчика управления, связанных с некоторой моделью программы. |
'''Модель''' - упрощённое описание реальности, выполненное с определенной целью. | '''Модель''' - упрощённое описание реальности, выполненное с определенной целью. | ||
| Строка 18: | Строка 18: | ||
# выбор языка моделирования | # выбор языка моделирования | ||
# абстракция системы до модели с учётом требований | # абстракция системы до модели с учётом требований | ||
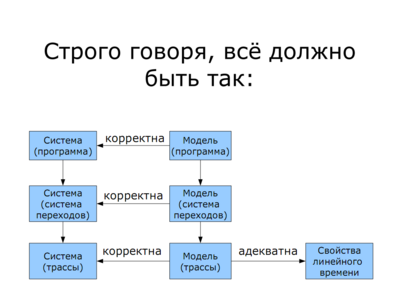
| + | [[Изображение:Verif2.png|400px|thumb|center|<u>Построение модели</u> в строгом смысле (''Лекция 2, слайд 38'')]] | ||
| + | |||
| + | Состояние называется <u>достижимым</u>, если существует вычисление программы, в котором оно присутствует | ||
=== Моделирование программ. Размеченные системы переходов. Детерминизм и недетерминизм. Вычисления и трассы. Свойства линейного времени. Выполнимость свойства на трассе.=== | === Моделирование программ. Размеченные системы переходов. Детерминизм и недетерминизм. Вычисления и трассы. Свойства линейного времени. Выполнимость свойства на трассе.=== | ||
| - | '''Размеченная система переходов (LTS) | + | '' Лекция 2, Слайды 39-50 '' |
| + | |||
| + | ====Размеченная система переходов (LTS)==== | ||
<math>TS = \langle S, Act, \overset{a}{\rightarrow} ,s_0, AP, L \rangle </math> | <math>TS = \langle S, Act, \overset{a}{\rightarrow} ,s_0, AP, L \rangle </math> | ||
| Строка 27: | Строка 32: | ||
* Act - множество действий | * Act - множество действий | ||
* '' <math>\tau</math> - невидимое действие '' | * '' <math>\tau</math> - невидимое действие '' | ||
| - | * <math>\overset{a}{\rightarrow} \subseteq S \times Act \times S </math> - тотальное отношение переходов | + | * <math>\overset{a}{\rightarrow} \subseteq S \times Act \times S </math> - тотальное отношение переходов. Тотальность означает, что из каждого состояния ведёт какое-то действие. |
| - | * <math>s_0 \in S</math> - начальное состояние | + | * <math>s_0 \in S</math> - начальное состояние, либо <math>I</math> - множество начальных состояний |
* AP - множество атомарных высказываний | * AP - множество атомарных высказываний | ||
* <math>L:S \rightarrow 2^{AP}</math> - функция разметки | * <math>L:S \rightarrow 2^{AP}</math> - функция разметки | ||
| Строка 36: | Строка 41: | ||
<math>\langle s, a, s' \rangle \in \overset{a}{\rightarrow} \equiv s \overset{a}{\rightarrow} s' </math> | <math>\langle s, a, s' \rangle \in \overset{a}{\rightarrow} \equiv s \overset{a}{\rightarrow} s' </math> | ||
| - | Пример LTS: Лекция 2, | + | ''Пример LTS: Лекция 2, слайды 40-41'' |
'''Прямые потомки''' | '''Прямые потомки''' | ||
| Строка 42: | Строка 47: | ||
* <math>Post(s) = \bigcup_{a \in Act} Post(s, a)</math> - все возможные состояния s', которые <u>непосредственно вытекают</u> из s | * <math>Post(s) = \bigcup_{a \in Act} Post(s, a)</math> - все возможные состояния s', которые <u>непосредственно вытекают</u> из s | ||
| - | Система <math>TS = | + | Система <math>TS = \langle S, Act, \overset{a}{\rightarrow} ,I, AP, L \rangle</math> '''детерминирована''': |
* '''по действиям''' тогда и только тогда, когда | * '''по действиям''' тогда и только тогда, когда | ||
** <math>|I| \leqslant 1</math> | ** <math>|I| \leqslant 1</math> | ||
| - | ** <math>\forall s \in S, \forall a \in Act \Rightarrow |Post(s, a)| \leqslant 1</math> | + | ** <math>\forall s \in S, \forall a \in Act \Rightarrow |Post(s, a)| \leqslant 1</math> (количество потомков не больше одного) |
* '''по атомарным высказываниям''' | * '''по атомарным высказываниям''' | ||
** <math>|I| \leqslant 1</math> | ** <math>|I| \leqslant 1</math> | ||
| - | ** <math>\forall s \in S, \forall A \in 2^{AP} ~ \Rightarrow ~ |Post(s) \cap \{s' \in S, L(s') = A\}| \leqslant 1</math> ( количество одинаково размеченных потомков не больше одного ) | + | ** <math>\forall s \in S, \forall A \in 2^{AP} ~ \Rightarrow ~ |Post(s) \cap \{s' \in S, L(s') = A\}| \leqslant 1</math> (количество '''одинаково размеченных''' потомков не больше одного) |
| - | ''' | + | '''Недетерминизм''' - это фича! Полезен для: |
* моделирования параллельного выполнения в режиме чередования (интерливинга) | * моделирования параллельного выполнения в режиме чередования (интерливинга) | ||
** позволяет не указывать скорость выполнения процессов | ** позволяет не указывать скорость выполнения процессов | ||
| Строка 59: | Строка 64: | ||
** модель может быть построена по неполной информации | ** модель может быть построена по неполной информации | ||
| - | + | ====Вычисления==== | |
| - | # '''Конечный фрагмент вычисления <math>\sigma</math>''' системы переходов TS | + | # '''Конечный фрагмент вычисления <math>\sigma</math>''' системы переходов TS - это конечная последовательность чередующихся состояний и действий, заканчивающаяся состоянием: <math>\sigma = s_0 a_1 s_1 a_2 s_2 \dots a_n s_n, \forall i \in [0,n) \Rightarrow s_i \overset{a_{i+1}}{\rightarrow} s_{i+1}</math> |
# '''Бесконечный (максимальный) фрагмент вычисления <math>\rho</math>''' - <math>\rho = s_0 a_1 s_1 a_2 s_2 \dots, \forall i \geqslant 0 \Rightarrow s_i \overset{a_{i+1}}{\rightarrow} s_{i+1}</math> | # '''Бесконечный (максимальный) фрагмент вычисления <math>\rho</math>''' - <math>\rho = s_0 a_1 s_1 a_2 s_2 \dots, \forall i \geqslant 0 \Rightarrow s_i \overset{a_{i+1}}{\rightarrow} s_{i+1}</math> | ||
# '''Начальный фрагмент вычисления''' - фрагмент вычисления, для которого <math>s_0 \in I</math> | # '''Начальный фрагмент вычисления''' - фрагмент вычисления, для которого <math>s_0 \in I</math> | ||
| - | # '''Вычисление''' - начальный максимальный фрагмент вычисления | + | # '''Вычисление''' - начальный максимальный фрагмент вычисления (описывает последовательность состояний и действий) |
'''Достижимое состояние''' (из начального) в системе переходов TS - такое состояние <math>s \in S</math>, для которого существует конечный фрагмент вычисления <math>s_0 a_1 s_1 a_2 s_2 \dots a_n s_n = s</math> | '''Достижимое состояние''' (из начального) в системе переходов TS - такое состояние <math>s \in S</math>, для которого существует конечный фрагмент вычисления <math>s_0 a_1 s_1 a_2 s_2 \dots a_n s_n = s</math> | ||
| - | ''' | + | '''Reach(TS)''' - множество всех достижимых состояний в TS |
| - | '''Трасса''' <math>tr = L(s_0) L(s_1) \dots \in (2^{AP})^\omega</math> | + | '''Трасса''' <math>tr = L(s_0) L(s_1) \dots \in (2^{AP})^\omega</math>; <math>~\omega</math> означает, что трасса может быть бесконечной |
| - | + | ====Свойства линейного времени==== | |
| - | * Свойство <math>\varphi</math> определяет набор допустимых трасс: <math>\varphi \ | + | * Свойство <math>\varphi</math> определяет набор допустимых трасс: <math>\varphi \subseteq (2^{AP})^\omega</math> |
| - | * Система переходов TS удовлетворяет свойству линейного времени <math>\varphi</math> | + | * Система переходов TS удовлетворяет свойству линейного времени <math>\varphi</math>, если: <math>TS \models \varphi ~~ \Leftrightarrow ~~ Traces(TS) \subseteq \varphi</math> |
| - | + | * по определению программа удовлетворяет свойству φ, если её система переходов удовлетворяет этому свойству: <math>P \models \varphi ~~ \equiv ~~ TS(P) \models \varphi </math> - | |
| - | * | + | |
=== Моделирование программ. Графы программ. Статическая и операционная семантика. === | === Моделирование программ. Графы программ. Статическая и операционная семантика. === | ||
| Строка 86: | Строка 90: | ||
** <math> dom(v) = D_p^v \subseteq D_p</math> -- каждая переменная принадлежит какому-либо домену | ** <math> dom(v) = D_p^v \subseteq D_p</math> -- каждая переменная принадлежит какому-либо домену | ||
* <math>n</math> -- подстановка. <math>n: V_p \rightarrow D_p, \forall v \in Var</math> <math>n(v) \in D_p^v</math> | * <math>n</math> -- подстановка. <math>n: V_p \rightarrow D_p, \forall v \in Var</math> <math>n(v) \in D_p^v</math> | ||
| - | * <math>Cond(V_p)</math> -- Набор булевых условий над <math>V_p</math> | + | * <math>~ Cond(V_p)</math> -- Набор булевых условий над <math>V_p</math> |
| - | ** формулы пропозициональной логики | + | ** формулы пропозициональной логики (<math>p1 \or p2</math>) |
| - | ** условия на переменные | + | ** условия на переменные вида <math>x \in X</math> (p1: 3<=y<18, p2: f=4) |
| + | * <math>~ Eval(Var)</math> -- множество значений переменных. Собственно, это и есть подстановка. | ||
* Эффект операторов: <math>Effect: Act \times Eval(Var) \rightarrow Eval(Var)</math> | * Эффект операторов: <math>Effect: Act \times Eval(Var) \rightarrow Eval(Var)</math> | ||
| Строка 95: | Строка 100: | ||
<math> PG= \langle Loc , Act , Effect ,\rightarrow, Loc_0, g_0 \rangle </math> | <math> PG= \langle Loc , Act , Effect ,\rightarrow, Loc_0, g_0 \rangle </math> | ||
| - | * <math>Loc</math> -- множество точек | + | * <math>~ Loc</math> -- множество точек |
** <math>Loc_0 \in Loc</math> -- множество начальных точек | ** <math>Loc_0 \in Loc</math> -- множество начальных точек | ||
| - | * <math>Act</math> -- множество действий | + | * <math>~ Act</math> -- множество действий |
| - | * <math>\rightarrow | + | * <math>\rightarrow \subseteq Loc \times (Cond(V_p) \times Act) \times Loc </math> -- отношение перехода (<math>Cond(V_p) </math> -- это фактически страж оператора ) |
| - | * <math>Effect</math> -- функция эффекта | + | * <math>~ Effect: Act \times Eval(Var) \rightarrow Eval(Var)</math> -- функция эффекта |
* <math>g_0 \in Cond(V_p)</math> -- начальное условие | * <math>g_0 \in Cond(V_p)</math> -- начальное условие | ||
| Строка 108: | Строка 113: | ||
** находимся в точке программы l | ** находимся в точке программы l | ||
** значение переменной x принадлежит некоторому множеству и это множество является подмножеством множеств значений этой переменной. | ** значение переменной x принадлежит некоторому множеству и это множество является подмножеством множеств значений этой переменной. | ||
| - | * Состояния <math> | + | * Состояния <math>\langle l,n \rangle</math> размечаются высказыванием о том, что мы находимся в точке программы <math>~ l</math> и всеми высказываниями, истинными в <math>~ n</math> |
| - | * Если в графе программы есть дуга из l в <math>l | + | * Если в графе программы есть дуга из <math>~ l</math> в <math>~ l'</math> со стражем <math>~ g</math> и действием <math>~ a</math> и в некоторой подстановке <math>~n</math> выполняется страж <math>~ g</math>, то в системе переходов, которая соответствует этой программе будет присутствовать дуга из состояния <math>\langle l,n\rangle</math> в состояние <math>\langle l', Effect(a,n)\rangle</math> по действию <math>~ a</math>. |
'''Системы переходов графов программ''' | '''Системы переходов графов программ''' | ||
| Строка 116: | Строка 121: | ||
* <math>S = Loc \times Eval(V_p)</math> (декартово произведение точек программы на всевозможные подстановки) | * <math>S = Loc \times Eval(V_p)</math> (декартово произведение точек программы на всевозможные подстановки) | ||
| - | * <math>\rightarrow : S \times Act \times S </math> с соответствующим правилом вывода <math>l \overset{g:a}{\rightarrow} l \and ( | + | * <math>\rightarrow : S \times Act \times S </math> с соответствующим правилом вывода <math> \frac{l \overset{g:a}{\rightarrow} l' \and (n \models g) }{\langle l,n \rangle \overset{a}{\rightarrow} \langle l',Effect(a,n) \rangle }</math> |
* Множество начальных состояний системы переходов описывается как множество состояний, в которых точка программы принадлежит начальным точкам, а на подстановках выполняется начальное условие графа программы: | * Множество начальных состояний системы переходов описывается как множество состояний, в которых точка программы принадлежит начальным точкам, а на подстановках выполняется начальное условие графа программы: | ||
| - | ** <math>I={\langle l , n \rangle : l \in Loc_0 , n | + | ** <math>I=\{\langle l , n \rangle : l \in Loc_0 , n \models g_0 \}</math> |
* Множество атомарных высказываний -- это объединение множества точек программы и всевозможных булевых высказываний над переменными программы: | * Множество атомарных высказываний -- это объединение множества точек программы и всевозможных булевых высказываний над переменными программы: | ||
** <math>AP=Loc \cup Cond(V_P) </math> | ** <math>AP=Loc \cup Cond(V_P) </math> | ||
| - | * Состояния вида <l,n> размечаются высказываниям о точке программы, в которой мы находимся и всеми высказываниями из множества всевозможных высказываний, которые верны в этой подстановке: | + | * Состояния вида <math>\langle l,n \rangle</math> размечаются высказываниям о точке программы, в которой мы находимся и всеми высказываниями из множества всевозможных высказываний, которые верны в этой подстановке: |
| - | ** <math>L(\langle l , n \rangle)= | + | ** <math>L(\langle l , n \rangle)= \{l\} \cup \{g \in Cond(V_P): n \models g \}.</math> |
| - | ''Пример: Лекция 4, слайд 16'' | + | '''Пример: Лекция 4, слайд 16''' |
| + | |||
| + | |||
| + | '''Статическая и операционная семантика''' | ||
| + | |||
| + | '''Cтатическая семантика''' – набор ограничений, которым должна удовлетворять структура программы; | ||
| + | '''Операционная семантика''' – понятие состояния программы и изменение состояния в ходе работы программы; то, как по графу строится LTS. | ||
| + | (См. Л.5, сл. 15, 2010 ) | ||
| + | |||
| + | === Параллелизм. Чередование систем переходов. === | ||
| + | ''Лекция 4, слайды 21-24'' | ||
| + | |||
| + | * Действия независимых процессов чередуются. | ||
| + | * Порядок выполнения процессов не известен. | ||
| + | |||
| + | '''Чередование:''' | ||
| + | * эффект от параллельного выполнения независимых действий a и b равен эффекту от их последовательного выполнения в произвольном порядке: | ||
| + | ** <math>Effect(a ~|||~ b,n) = Effect((a;b)+(b;a),n)</math> | ||
| + | *** ||| -- оператор чередования | ||
| + | *** ; -- оператор последовательного выполнения | ||
| + | *** + -- оператор недетерминированного выбора | ||
| + | |||
| + | ''Пример: Лекция 4, слайд 23'' | ||
| + | |||
| + | '''Чередование систем переходов''' | ||
| + | |||
| + | Пусть <math>TS_i = \langle S_i, Act_i, \rightarrow_i, AP_i, I_i, L_i \rangle ~~,~~ i \in \{1,2\}</math> | ||
| + | |||
| + | Тогда чередование этих систем <math>TS_1 ~|||~ TS_2= \langle S_1 \times S_2, Act_1 \cup Act_2, \rightarrow, AP_1 \cup AP_2, I_1 \times I_2, L \rangle</math>, где | ||
| + | * <math>L(s_1, s_2)= L_1(s_1) \cup L_2(s_2) </math> | ||
| + | * оператор <math>\rightarrow</math> определяется как | ||
| + | ** <math>\frac{s_1 \rightarrow_1 s_1^'}{(s_1, s_2) \rightarrow (s_1^', s_2)}</math> | ||
| + | ** <math>\frac{s_2 \rightarrow_2 s_2^'}{(s_1, s_2) \rightarrow (s_1, s_2^')}</math> | ||
| - | === Параллелизм. Чередование систем переходов. === | ||
=== Параллелизм. Чередование графов программ. Случаи без разделяемых переменных и с разделяемыми переменными. === | === Параллелизм. Чередование графов программ. Случаи без разделяемых переменных и с разделяемыми переменными. === | ||
| + | '' Лекция 4, слайды 25—28 '' | ||
| + | |||
| + | Для графов программ <math>PG_1</math> (над <math>V_1</math>) и <math>PG_2</math> (над <math>V_2</math>) без разделяемых переменных (т. е. <math>V_1 \cap V_2 = \varnothing</math>): | ||
| + | * формула <math>TS(PG_1)~|||~TS(PG_2)</math> достоверно описывает параллельную композицию <math>PG_1</math> и <math>PG_2</math> | ||
| + | * в случае с разделяемыми переменными это не так (см. лекцию 4, слайд 26). | ||
| + | |||
| + | Пусть | ||
| + | :<math>PG_i = \langle Loc_i, Act_i, Effect_i, \rightarrow_i, Loc_{0,i}, g_{0,i} \rangle,~i \in \{1, 2\}.</math> | ||
| + | Граф <math>PG_1~|||~PG_2</math> над <math>V_1 \cup V_2</math> определяется так: | ||
| + | :<math>PG_1~|||~PG_2 = \langle Loc_1 \times Loc_2, Act_1 \cup Act_2, Effect, \rightarrow, Loc_{0,1} \times Loc_{0,2}, g_{0,1} \land g_{0,2} \rangle,</math> | ||
| + | где отношение перехода <math>\rightarrow</math> определяется следующими правилами вывода: | ||
| + | :<math>l_1 \overset{g:\alpha}{\rightarrow}_1 l'_1 \over \langle l_1, l_2 \rangle \overset{g:\alpha}{\rightarrow} \langle l'_1, l_2 \rangle</math> и <math>l_2 \overset{g:\alpha}{\rightarrow}_2 l'_2 \over \langle l_1, l_2 \rangle \overset{g:\alpha}{\rightarrow} \langle l_1, l'_2 \rangle,</math> | ||
| + | а <math>Effect(\alpha,~\eta) = Effect_i(\alpha,~\eta),</math> если <math>\alpha \in Act_i.</math> | ||
| + | |||
| + | ''Пример: лекция 4, слайд 28.'' В указанном примере <math>TS(PG_1)~|||~TS(PG_2) \neq TS(PG_1~|||~PG_2)</math> | ||
| + | |||
=== Параллелизм. Синхронный параллелизм. Рандеву. === | === Параллелизм. Синхронный параллелизм. Рандеву. === | ||
* распределённые программы выполняются параллельно | * распределённые программы выполняются параллельно | ||
| Строка 136: | Строка 188: | ||
<u>Передача сообщений в распределённых программах:</u> | <u>Передача сообщений в распределённых программах:</u> | ||
* cинхронная передача сообщений (рандеву) | * cинхронная передача сообщений (рандеву) | ||
| - | * асинхронная передача сообщений ( | + | * асинхронная передача сообщений (каналы) |
| - | <u>Синхронный обмен | + | <u>Синхронный обмен сообщениями:</u> |
* Процессы вместе выполняют синхронизированные действия | * Процессы вместе выполняют синхронизированные действия | ||
* Взаимодействие процессов - одновременно | * Взаимодействие процессов - одновременно | ||
| Строка 144: | Строка 196: | ||
'''Рандеву''' | '''Рандеву''' | ||
* <math>TS_i = \langle S_i, Act_i, \overset{a}{\rightarrow}_i ,I_i, AP_i, L_i \rangle ~~~ i=\{1,2\}</math> | * <math>TS_i = \langle S_i, Act_i, \overset{a}{\rightarrow}_i ,I_i, AP_i, L_i \rangle ~~~ i=\{1,2\}</math> | ||
| - | * <math>H \subseteq Act_1 \cap Act_2</math> | + | * <math>H \subseteq Act_1 \cap Act_2</math> -- набор синхронизированных действий. |
| + | ** действия из H должны быть синхронизированны | ||
| + | ** действия не из H независимы и могут чередоваться | ||
| - | Тогда <math>TS_1 ||_H = \langle S_1 \times S_2, Act_1 \cup Act_2, \rightarrow, I_1 \times I_2, AP_1 \cup AP_2, L \rangle</math>, где | + | Тогда <math>TS_1 ||_H TS_2= \langle S_1 \times S_2, Act_1 \cup Act_2, \rightarrow, I_1 \times I_2, AP_1 \cup AP_2, L \rangle</math>, где |
* <math>L(\langle s_1, s_2 \rangle) = L_1(s_1) \cup L_2(s_2)</math> | * <math>L(\langle s_1, s_2 \rangle) = L_1(s_1) \cup L_2(s_2)</math> | ||
* <math>\rightarrow</math> определяется как: | * <math>\rightarrow</math> определяется как: | ||
** интерливинг для <math>\alpha \not\in H~:~~~ \frac{s_1 \overset{a}{\rightarrow}_1 s_1'}{ \langle s_1, s_2 \rangle \overset{a}{\rightarrow} \langle s_1', s_2 \rangle}</math> и <math>\frac{s_2 \overset{a}{\rightarrow}_2 s_2'}{ \langle s_1, s_2 \rangle \overset{a}{\rightarrow} \langle s_1, s_2' \rangle}</math> | ** интерливинг для <math>\alpha \not\in H~:~~~ \frac{s_1 \overset{a}{\rightarrow}_1 s_1'}{ \langle s_1, s_2 \rangle \overset{a}{\rightarrow} \langle s_1', s_2 \rangle}</math> и <math>\frac{s_2 \overset{a}{\rightarrow}_2 s_2'}{ \langle s_1, s_2 \rangle \overset{a}{\rightarrow} \langle s_1, s_2' \rangle}</math> | ||
| - | ** рандеву для <math>\alpha \in H~:~~~ \frac{s_1 \overset{a}{\rightarrow}_1 s_1' ~ \wedge ~ s_2 \overset{a}{\rightarrow}_2 s_2'}{ \langle s_1, s_2 \rangle \overset{a}{\rightarrow} \langle s_1', s_2 \rangle}</math> | + | ** рандеву для <math>\alpha \in H~:~~~ \frac{s_1 \overset{a}{\rightarrow}_1 s_1' ~ \wedge ~ s_2 \overset{a}{\rightarrow}_2 s_2'}{ \langle s_1, s_2 \rangle \overset{a}{\rightarrow} \langle s_1', s_2' \rangle}</math> |
| Строка 162: | Строка 216: | ||
Тогда <math>TS_1 \times TS_2 = \langle S_1 \times S_2, Act, \rightarrow, I_1 \times I_2, AP_1 \cup AP_2, L \rangle </math>, где | Тогда <math>TS_1 \times TS_2 = \langle S_1 \times S_2, Act, \rightarrow, I_1 \times I_2, AP_1 \cup AP_2, L \rangle </math>, где | ||
* <math>L(\langle s_1, s_2 \rangle) = L_1(s_1) \cup L_2(s_2)</math> | * <math>L(\langle s_1, s_2 \rangle) = L_1(s_1) \cup L_2(s_2)</math> | ||
| - | * <math>\rightarrow</math> определяется как: <math>\frac{s_1 \overset{\alpha}{\rightarrow}_1 s_1' ~ \wedge ~ s_2 \overset{\beta}{\rightarrow}_2 s_2'}{ \langle s_1, s_2 \rangle \overset{\alpha * \beta}{\rightarrow} \langle s_1', s_2 \rangle}</math> | + | * <math>\rightarrow</math> определяется как: <math>\frac{s_1 \overset{\alpha}{\rightarrow}_1 s_1' ~ \wedge ~ s_2 \overset{\beta}{\rightarrow}_2 s_2'}{ \langle s_1, s_2 \rangle \overset{\alpha * \beta}{\rightarrow} \langle s_1', s_2' \rangle}</math> |
=== Параллелизм. Асинхронный параллелизм. Системы с каналами. Операционная семантика. === | === Параллелизм. Асинхронный параллелизм. Системы с каналами. Операционная семантика. === | ||
| + | |||
| + | ''Лекция 4. Слайды 36-39, 43-46 '' | ||
| + | |||
| + | * <math>c \in Chan</math> -- Процессы взаимодействуют с помощью '''каналов''', представляющих собой FIFO буфера | ||
| + | * <math>dom(c)</math> -- Каналы типизированы по передаваемым сообщениям | ||
| + | * <math>cap(c)</math> -- ёмкость канала. если <math>cap(c) = 0</math>, то взаимодействие сводится к рандеву | ||
| + | * действия по обмену сообщениями: | ||
| + | ** <math>c!v</math> -- запись <math>v</math> в конец канала <math>c</math>. Выполняется только если буфер не полон (<math> < cap(c)</math>) | ||
| + | ** <math>c?x</math> -- чтение в <math>x</math> из начала канала <math>c</math>. Выполняется только если буфер не пуст (<math> > cap(c)</math>) | ||
| + | ** формально <math>Comm = \{c!v, c?x ~ | ~ c \in Chan, v \in dom(c), x \in V_p, dom(c) \subseteq dom(x)\}</math> | ||
| + | |||
| + | <u>Системы с каналами.</u> | ||
| + | * Граф программы <math>PG</math> над <math>(Var, Chan)</math> задаётся <math>PG = \langle Loc, Act, Effect, \rightarrow, Log_0, g_0 \rangle</math>, где <math>\rightarrow \subseteq Loc \times (Cond(Var) \times Act) \times Loc ~ \cup ~ Loc \times Comm \times Loc</math> | ||
| + | * Система с каналами <math>CS</math> над <math>\left(\cup_{1 \leqslant i \leqslant n} PG_i, Chan\right)</math> задаётся как <math>CS = \left[PG_1 | PG_2 | \dots | PG_n\right]</math>, где <math>PG_i</math> — граф программы над <math>(Var_i, Chan)</math> | ||
| + | |||
| + | При асинхронной передаче сообщений (при <math>cap(c) > 0</math>): | ||
| + | * процесс <math>P_i</math> может выполнить <math>l_i \overset{c!v}{\rightarrow} l'_i</math>, только если в <math>c</math> хранится меньше <math>cap(c)</math> сообщений; | ||
| + | * процесс <math>P_j</math> может выполнить <math>l_j \overset{c?x}{\rightarrow} l'_j</math>, только если <math>c</math> не пуст, после чего первый элемент <math>v</math> извлекается из <math>c</math> и присваивается <math>x</math> (атомарно). | ||
| + | |||
| + | '''Оценка <math>\xi</math> значения канала''' <math>c</math> — это отображение канала на последовательность значений <math>\xi: Chan \rightarrow dom(c)^*</math>, такое что длина последовательности не превосходит ёмкости канала <math>len(\xi(c)) \leq cap(c)</math>, и при этом <math>\xi(c)=v_1 v_2 \dots v_k</math> означает, что <math>v_1</math> — верхнее сообщение в буфере. | ||
| + | :<math>\xi[c = v_1 v_2 \dots v_k](c') = \left\{ \begin{array}{cc} | ||
| + | \xi(c'), & c \neq c' \\ | ||
| + | v_1 v_2 \dots v_k, & c = c' \\ | ||
| + | \end{array} \right.</math> ''Кто понимает смысл этой хренотени, опишите, плз. [[Участник:Overrider|Overrider]] 18:28, 22 мая 2009 (UTC)'' | ||
| + | |||
| + | Исходная оценка <math>\xi_0(c) = \epsilon, \forall c \in Chan</math> | ||
| + | |||
| + | ''Операционная семантика: лекция 4, слайды 44—46'' | ||
| + | |||
| + | ====операционная семантика==== | ||
| + | |||
| + | Пусть <math>CS = \left[PG_1 | PG_2 | \dots | PG_n\right]</math> – система с каналами над <math>(Chan, Var)</math>, и | ||
| + | |||
| + | <math>PG = \langle Loc, Act, Effect, \rightarrow, Log_0, g_0 \rangle</math> | ||
| + | |||
| + | Система переходов <math>TS(CS)</math> описывается сигнатурой | ||
| + | |||
| + | <math>TS(CS) = \langle S, Act, \rightarrow, I , AP, L \rangle </math>, где | ||
| + | |||
| + | <math>S = ( Loc_1 \times \dots \times Loc_n ) \times Eval(Var) \times Eval(Chan)</math> | ||
| + | |||
| + | <math>Act = ( \cup_{0 \leqslant i \leqslant n} Act_i ) ~ \cup ~ \tau </math> | ||
| + | |||
| + | <math>I = \{ | ||
| + | \langle | ||
| + | l_1, \dots, l_n, \eta, \xi | ||
| + | \rangle | ||
| + | | | ||
| + | \forall i ( l_i \in Loc_{0i} \and \eta \models g_0 ) \and \forall c ( \xi_0(c) = \epsilon ) | ||
| + | \}</math> | ||
| + | |||
| + | <math>AP = ( \cup_{0 \leqslant i \leqslant n} Loc_i ) \cup Cond(Var)</math> | ||
| + | |||
| + | <math>L( | ||
| + | \langle | ||
| + | l_1, \dots, l_n, \eta, \xi | ||
| + | \rangle | ||
| + | ) = | ||
| + | \{ | ||
| + | l_1, \dots, l_n | ||
| + | \} | ||
| + | \cup | ||
| + | \{ | ||
| + | g \in Cond( Var ) | \eta \models g | ||
| + | \}</math> | ||
| + | |||
| + | '''Правила вывода''' | ||
| + | <ul> | ||
| + | <li> <p> интерливинг для <math> \alpha \in Act_i </math> </p> | ||
| + | <p><math> | ||
| + | \frac | ||
| + | {l_i \overset{g:\alpha}{\rightarrow} l_i' \and n \models g } | ||
| + | { | ||
| + | \langle | ||
| + | l_1, \dots , l_i, \dots , l_n , \eta, \xi | ||
| + | \rangle | ||
| + | \overset{\alpha}{\rightarrow} | ||
| + | \langle | ||
| + | l_1, \dots, l_i', \dots, l_n , \eta', \xi | ||
| + | \rangle | ||
| + | } | ||
| + | </math></p> | ||
| + | |||
| + | </li> | ||
| + | <li> <p>Синхронная передача сообщений через <math>c \in Chan, cap(c) = 0</math></p> | ||
| + | |||
| + | <p> | ||
| + | <math> | ||
| + | \frac | ||
| + | { | ||
| + | l_i \overset{c?x}{\rightarrow} l_i' \and | ||
| + | l_j \overset{c!v}{\rightarrow} l_j' \and | ||
| + | i \neq j | ||
| + | } | ||
| + | { | ||
| + | \langle | ||
| + | l_1, \dots , l_i, \dots, l_j, \dots , l_n , \eta, \xi | ||
| + | \rangle | ||
| + | \overset{\alpha}{\rightarrow} | ||
| + | \langle | ||
| + | l_1, \dots, l_i', \dots, l_j', \dots , l_n , \eta', \xi | ||
| + | \rangle | ||
| + | } | ||
| + | </math> | ||
| + | </p> | ||
| + | </li> | ||
| + | <li> | ||
| + | <p> | ||
| + | Асинхронная передача сообщений через <math>c \in Chan, cap(c) \neq 0</math> | ||
| + | </p> | ||
| + | <ul> | ||
| + | <li> | ||
| + | <p> | ||
| + | получить значение по каналу c и присвоить переменной x: | ||
| + | </p> | ||
| + | |||
| + | <p> | ||
| + | <math> | ||
| + | \frac | ||
| + | { | ||
| + | l_i \overset{c?x}{\rightarrow} l_i' \and | ||
| + | len(\xi(c))=k>0) \and | ||
| + | \xi(c)=v_1 \dots vk | ||
| + | } | ||
| + | { | ||
| + | \langle | ||
| + | l_1, \dots , l_i, \dots , l_n , \eta, \xi | ||
| + | \rangle | ||
| + | \overset{c?x}{\rightarrow} | ||
| + | \langle | ||
| + | l_1, \dots, l_i', \dots, l_n , \eta', \xi' | ||
| + | \rangle | ||
| + | } | ||
| + | </math>, | ||
| + | </p> | ||
| + | |||
| + | <p> | ||
| + | где | ||
| + | <math> | ||
| + | \eta' = \eta[x=v_1], \xi'=\xi[c=v_2 \dots v_k ] | ||
| + | </math> | ||
| + | </p> | ||
| + | |||
| + | </li> | ||
| + | |||
| + | <li> | ||
| + | <p> | ||
| + | передать значение <math>v \in dom(c) </math> по каналу c: | ||
| + | </p> | ||
| + | <p> | ||
| + | <math> | ||
| + | \frac | ||
| + | { | ||
| + | l_i \overset{c!v}{\rightarrow} l_i' \and | ||
| + | len(\xi(c))=k<cap(c)) \and | ||
| + | \xi(c)=v_1 \dots vk | ||
| + | } | ||
| + | { | ||
| + | \langle | ||
| + | l_1, \dots , l_i, \dots , l_n , \eta, \xi | ||
| + | \rangle | ||
| + | \overset{c!v}{\rightarrow} | ||
| + | \langle | ||
| + | l_1, \dots, l_i', \dots, l_n , \eta, \xi' | ||
| + | \rangle | ||
| + | } | ||
| + | </math>, | ||
| + | </p> | ||
| + | <p> | ||
| + | где | ||
| + | <math> | ||
| + | \xi'=\xi[c=v_1 \dots v_k v ] | ||
| + | </math> | ||
| + | </p> | ||
| + | </li> | ||
| + | </ul> | ||
| + | </li> | ||
| + | </ul> | ||
| + | |||
| + | <math></math> | ||
| + | <math></math> | ||
| + | |||
=== Абстракция. Абстракция трасс. Абстракция системы переходов. Необходимое и достаточное условие корректности LTS модели. === | === Абстракция. Абстракция трасс. Абстракция системы переходов. Необходимое и достаточное условие корректности LTS модели. === | ||
| - | Представим трассу в форме интерпретации I: <math>I(tr) = | + | Представим трассу в форме интерпретации I: <math>I(tr) = \langle\mathbb{N}, \leqslant, \xi\rangle</math> |
| - | * <math>N</math> - множество натуральных чисел | + | * <math>\mathbb{N}</math> - множество натуральных чисел |
| - | * <math>\leqslant</math> - отношение порядка на <math>N</math> | + | * <math>\leqslant</math> - отношение порядка на <math>\mathbb{N}</math> |
| - | * <math>\xi: N \times AP \rightarrow \{true, false\}, ~~ \forall n>0, p \in AP ~~ \Rightarrow ~~ \xi(n, p) = true \Leftrightarrow p \in L(s)</math> | + | * <math>\xi: \mathbb{N} \times AP \rightarrow \{true, false\}, ~~ \forall n>0, p \in AP ~~ \Rightarrow ~~ \xi(n, p) = true \Leftrightarrow p \in L(s)</math> (для каждого порядкового номера говорит истенен или ложен заданный на нем предикат) |
Рассмотрим трассы tr и tr' такие, что | Рассмотрим трассы tr и tr' такие, что | ||
| - | * <math>I(tr) = | + | * <math>I(tr) = \langle\mathbb{N}, \leqslant, \xi\rangle, ~~ \xi: \mathbb{N} \times AP = \{true, false\}</math> |
| - | * <math>I(tr) = | + | * <math>I(tr') = \langle\mathbb{N}, \leqslant, \xi'\rangle, ~~ \xi: \mathbb{N} \times AP' = \{true, false\}</math> |
| - | Будем говорить, что трасса tr' является '''абстракцией трассы''' tr, если | + | Будем говорить, что трасса tr' является '''абстракцией трассы''' tr (<math>tr \prec tr'</math>), если |
# <math>AP' \subseteq AP</math> | # <math>AP' \subseteq AP</math> | ||
| - | # <math>\exists \alpha : N \rightarrow N</math> такое, что <math>\forall n,k \in N, n \leqslant k ~~ \Rightarrow ~~ \alpha(n) \leqslant \alpha(k) </math> | + | # <math>\exists \alpha : \mathbb{N} \rightarrow \mathbb{N}</math> такое, что |
| - | # <math>\forall n \in N, p \in AP' ~~ \Rightarrow ~~ \xi(n, p) = \xi'(n, p)</math> | + | #* <math>\alpha</math> - неубывающая функция: <math>\forall n,k \in \mathbb{N}, n \leqslant k ~~ \Rightarrow ~~ \alpha(n) \leqslant \alpha(k) </math> |
| + | #* <math>\forall n \in \mathbb{N}, p \in AP' ~~ \Rightarrow ~~ \xi(n, p) = \xi'(\alpha(n), p)</math> | ||
Пример абстракции трассы: Лекция 2, слайд 53 | Пример абстракции трассы: Лекция 2, слайд 53 | ||
| - | ''' | + | '''Определение.''' Пусть P – система, φ – произвольное свойство линейного времени. '''Корректной моделью ''' P называется такая М, что: |
| - | + | <math> M \models \phi \Rightarrow P \models \phi </math>. | |
| - | + | ''(позволяет проверять свойства программы на её модели )'' | |
| - | + | ''' Необходимое и достаточное условие корректности модели:''' | |
| + | Модель <math>M</math> системы <math>P</math> корректна тогда и только тогда, когда <math>\forall tr \in Traces(TS(P)) ~ \exists tr' \in Traces(TS(M)) ~ : ~ tr \prec tr'</math>. | ||
| + | ''(для проверки такого условия нужно рассмотреть все трассы исходной системы, допускает, что в модели | ||
| + | больше состояний )'' | ||
=== Абстракция. Абстракция системы переходов. Достаточное условие корректности LTS модели. Адекватность LTS модели. === | === Абстракция. Абстракция системы переходов. Достаточное условие корректности LTS модели. Адекватность LTS модели. === | ||
| Строка 199: | Строка 439: | ||
Достаточное условие корректности: | Достаточное условие корректности: | ||
| - | * Алфавит предикатов модели включен в алафвит предикатов системы: <math>AP^2 \ | + | * Алфавит предикатов модели включен в алафвит предикатов системы: <math>AP^2 \sube AP^1 </math> |
* Задано отображение <math>a: S^1 \rightarrow S^2</math>. На отображение накладываются следующие условия: | * Задано отображение <math>a: S^1 \rightarrow S^2</math>. На отображение накладываются следующие условия: | ||
** Оно преобразует начальное состояние системы в начальное состояние модели: <math>s^2_0 = a(s^1_0)</math> | ** Оно преобразует начальное состояние системы в начальное состояние модели: <math>s^2_0 = a(s^1_0)</math> | ||
** Каждому переходу из системы должен соответствовать переход в модели: <math>s^1_1 \rightarrow_1 s^1_2 ~ \Rightarrow ~ a(s^1_1) \rightarrow_2 a(s^1_2)</math> | ** Каждому переходу из системы должен соответствовать переход в модели: <math>s^1_1 \rightarrow_1 s^1_2 ~ \Rightarrow ~ a(s^1_1) \rightarrow_2 a(s^1_2)</math> | ||
| - | * Метки на состояниях модели должны состоять только из предикатов модели: <math>\forall s \in S^1: L^2(a(s)) = L^1(s) \cap AP^ | + | * Метки на состояниях модели должны состоять только из предикатов модели: <math>\forall s \in S^1: L^2(a(s)) = L^1(s) \cap 2^{AP^2}</math> |
| - | ''' | + | Модель называется '''адекватной''', если: |
| + | * Атомарные высказывания, в терминах которых задаются свойства, присутствуют в разметке модели. ''(Необходимое условие)'' | ||
| + | * Из нарушения свойства на модели следует, что оно нарушается и на исходной системе. ''(Достаточное условие)'' | ||
| - | + | '''Необходимое условие адекватности модели свойствам правильности''': алфавит предикатов свойств правильности включен в алфавит предикатов модели — <math>AP_\phi \subseteq AP_M</math>. Условие не является достаточным (см. примеры, лекция 3, слайды 4—5). | |
=== Абстракция. Абстракция графов программ. Отношение слабой симуляции. === | === Абстракция. Абстракция графов программ. Отношение слабой симуляции. === | ||
| + | Лекция 10, слайды 8 - 11 | ||
| + | Программа PG' ''корректно моделирует'' программу PG тогда и только тогда, когда система переходов TS(PG') корректно моделирует систему переходов TS(PG). | ||
| + | |||
| + | Будем говорить, что PG' моделирует PG, если | ||
| + | * в PG' присутствуют переменные, соответствующие наблюдаемым переменным PG | ||
| + | * все действия PG, влияющие на наблюдаемые переменные, отражены в модели <i>(наблюдаемые операторы)</i> | ||
| + | * модель корректно воспроизводит возможные последовательности изменения значений наблюдаемых переменных, присутствующих в PG | ||
| + | |||
| + | '''Отношение слабой симуляции''' не сохраняет количество шагов между состояниями. В связи с этим, не сохраняются свойства, не инвариантные к | ||
| + | прореживанию (LTL: оператор neXt). | ||
== Логика LTL, автоматы Бюхи == | == Логика LTL, автоматы Бюхи == | ||
=== Свойства правильности. Формулирование требований правильности программы. Двойственность. Типы свойств. === | === Свойства правильности. Формулирование требований правильности программы. Двойственность. Типы свойств. === | ||
| + | ''Лекция 5, слайды 2-14.'' | ||
| - | '''Требования правильности''' | + | '''Требования правильности''' — утверждения о возможных и невозможных вариантах выполнения программы. |
<u>Двойственность</u> : | <u>Двойственность</u> : | ||
| - | * если какое-то утверждение невозможно, то обратное | + | * если какое-то утверждение невозможно, то обратное — неизбежно |
| - | * если какое-то утверждение неизбежно, то обратное | + | * если какое-то утверждение неизбежно, то обратное — невозможно |
* при помощи логики от одного можно переходить к другому при помощи отрицания | * при помощи логики от одного можно переходить к другому при помощи отрицания | ||
| - | |||
| - | ''Схема верификации на модели: Лекция 2, слайд 3'' | ||
| - | |||
| - | <u>Примеры классов свойств:</u> | ||
| - | * Стандартные | ||
| - | ** [http://en.wikipedia.org/wiki/Deadlock deadlocks] ([http://ru.wikipedia.org/wiki/%D0%92%D0%B7%D0%B0%D0%B8%D0%BC%D0%BD%D0%B0%D1%8F_%D0%B1%D0%BB%D0%BE%D0%BA%D0%B8%D1%80%D0%BE%D0%B2%D0%BA%D0%B0 взаимная блокировка]) | ||
| - | ** [http://en.wikipedia.org/wiki/Race_condition Race condition] ([http://ru.wikipedia.org/wiki/%D0%A1%D0%BE%D1%81%D1%82%D0%BE%D1%8F%D0%BD%D0%B8%D0%B5_%D0%B3%D0%BE%D0%BD%D0%BA%D0%B8 состояние гонки]) | ||
| - | * Специфичные для конкретного приложения | ||
| - | ** требования справедливости | ||
| - | ** корректная завершаемость | ||
| - | ** причинно-следственный и темпоральный порядок состояний системы | ||
<u>Способы описания свойств правильности:</u> | <u>Способы описания свойств правильности:</u> | ||
| Строка 239: | Строка 481: | ||
* в Promela: | * в Promela: | ||
** свойства состояний | ** свойства состояний | ||
| - | *** asserts | + | *** [http://en.wikipedia.org/wiki/Assertion_%28computing%29 asserts]: |
**** локальные ассерты процессов | **** локальные ассерты процессов | ||
| - | **** инварианты системы процессов | + | **** [http://ru.wikipedia.org/wiki/%D0%98%D0%BD%D0%B2%D0%B0%D1%80%D0%B8%D0%B0%D0%BD%D1%82#.D0.98.D0.BD.D0.B2.D0.B0.D1.80.D0.B8.D0.B0.D0.BD.D1.82.D1.8B_.D0.B2_.D0.BF.D1.80.D0.BE.D0.B3.D1.80.D0.B0.D0.BC.D0.BC.D0.B8.D1.80.D0.BE.D0.B2.D0.B0.D0.BD.D0.B8.D0.B8 инварианты] системы процессов |
*** метки терминальных состояний | *** метки терминальных состояний | ||
**** задаём допустимые точки останова прочесса | **** задаём допустимые точки останова прочесса | ||
** свойства последовательностей состояний | ** свойства последовательностей состояний | ||
| - | *** метки прогресса | + | *** метки прогресса — чтобы найти циклы бездействия |
| - | *** утверждения о невозможности (never claims) | + | *** утверждения о невозможности (never claims) — например, LTL формулы |
| - | *** трассовые ассерты | + | *** трассовые ассерты — используются для описания правильных последовательностей выполнения операторов отправки и приема сообщения |
=== Свойства правильности. Свойства безопасности и живучести. Проверка таких свойств. Примеры свойств. === | === Свойства правильности. Свойства безопасности и живучести. Проверка таких свойств. Примеры свойств. === | ||
| Строка 260: | Строка 502: | ||
** пример: “отзывчивость” (например, если отправлен запрос, то рано или поздно будет сгенерирован ответ) | ** пример: “отзывчивость” (например, если отправлен запрос, то рано или поздно будет сгенерирован ответ) | ||
** задача верификатора – найти вычисления, в которых это “хорошее” может откладываться до бесконечности. | ** задача верификатора – найти вычисления, в которых это “хорошее” может откладываться до бесконечности. | ||
| + | '''ps'''. автор терминов – Лесли Лампорт; см. ''Лекция 5, слайд 4''. | ||
=== Автоматы Бюхи. Конечные автоматы. Проход автомата. Язык автомата. === | === Автоматы Бюхи. Конечные автоматы. Проход автомата. Язык автомата. === | ||
| + | ''Лекция 6, слайды 8 - 15'' | ||
| + | |||
| + | '''Конечный автомат''' | ||
| + | описывается сигнатурой: <math>\langle S, s_0, L, F, T\rangle</math>, где | ||
| + | |||
| + | * S -- множество сотояний | ||
| + | * <math>s_0 \in S </math> -- множество начальных состояний | ||
| + | * L -- конечное множество меток | ||
| + | * <math>F \subseteq S </math> -- множество терминальных состояний | ||
| + | * <math>T \subseteq S \times L \times S</math> -- отношение перехода на состояниях | ||
| + | ''' | ||
| + | Детерминизм и недетерминизм''' | ||
| + | |||
| + | Конечный автомат называется '''детерминированным''', если по метке и исходному состоянию можно однозначно определить целевое состояние: | ||
| + | <math>\forall s \in S, \forall l \in L: ((s, l, s_1) \in A.T \and (s, L, s_2) \in A.T ~ \Rightarrow ~ s_1 = s_2) </math> | ||
| + | |||
| + | В противном случае автомат называется '''недетерминированным'''. | ||
| + | |||
| + | '''Проходом a конечного автомата''' <math>\langle S,s_0,L,F,T \rangle</math> называется такое ''упорядоченное'' и, возможно, бесконечное множеств переходов из T: | ||
| + | <math>a=\langle (s_0, l_0, s_1),(s_1, l_1, s_2), ... \rangle ~~ \forall i, i \geqslant 0;~ (s_i, l_{i}, s_{i+1}) \in T</math> | ||
| + | |||
| + | |||
| + | '''Допускающим проходом''' конечного автомата A называется конечный проход a, финальный переход которого | ||
| + | (<math>s_{n-1},l_{n-1},s_n)</math> ведёт в терминальное состояние. | ||
| + | |||
| + | '''Языком автомата A''' называется множество слов в алфавите A.L, соответствующих допускающим проходам автомата А | ||
| + | |||
=== Автоматы Бюхи. Омега-допускание. Расширение автоматов Бюхи. === | === Автоматы Бюхи. Омега-допускание. Расширение автоматов Бюхи. === | ||
| + | ''Лекция 6, слайды 19-20'' | ||
| + | |||
| + | Для любого бесконечного прохода <math>\sigma</math> конечного автомата А можно выделить два последовательных отрезка проходов: | ||
| + | * <math>\sigma^{+}</math> -- конечный отрезок прохода <math>\sigma</math>, включающий в себя множество состояний, встречающихся конечное число раз | ||
| + | * <math>\sigma^\omega</math> -- бесконечный хвост прохода <math>\sigma</math>, включающий в себя множество состояний, встречающихся бесконечное число раз | ||
| + | |||
| + | '''Допускающий проход по Бюхи''' (<math>\omega</math>-допускание) конечного автомата A называется такой ''бесконечный проход'', в котором по крайней мере одно терминальное состояние встречается бесконечное число раз: <math>\exists i \geqslant 0, (s_{i-1}, l_{i-1}, s_i) \in \sigma ~~ : ~~ (s_{i} \in A.F) \and (s_{i} \in \sigma^\omega) </math> | ||
| + | |||
| + | <u>Расширение автоматов Бюхи.</u> | ||
| + | * добавляем алфавит автомата меткой <math>\varepsilon</math> | ||
| + | * все конечные проходы расширяем до бесконечности меткой <math>\varepsilon</math> | ||
| + | |||
| + | Примечание. При помощи автоматов Бюхи удобно проверять свойства живучести. | ||
| + | |||
=== Логика LTL. Синтаксис LTL. Семантика выполнимости формул. Сильный и слабый until. === | === Логика LTL. Синтаксис LTL. Семантика выполнимости формул. Сильный и слабый until. === | ||
| + | '' Лекция 6, слайды 30 - 35'' | ||
| + | |||
| + | |||
| + | <u>Особенности LTL:</u> | ||
| + | * может использоваться для описания свойств как живучести, так и безопасности | ||
| + | * описывает свойства, которым должны удовлетворять линейные последовательности наблюдаемых состояний - трассы | ||
| + | * семантика LTL определена на бесконечных автоматах Бюхи. Для конечных проходов необходимо использовать расширение автомата. | ||
| + | |||
| + | <u>Формула в LTL '''f::='''</u> | ||
| + | * '''p, q, ... ''' — свойства состояний, включая '''true''' и '''false''' | ||
| + | * '''(f)''' — группировка при помощи скобок | ||
| + | * '''<math>\alpha ~ f</math>''' — унарные операторы | ||
| + | * '''<math>f_1 ~ \beta ~ f_2</math>''' — бинарные операторы | ||
| + | |||
| + | <u>Операторы в LTL</u> | ||
| + | * унарные | ||
| + | ** <math>\Box</math> ([]) — всегда в будущем, т.е. <math>s_j \models \Box f ~~~ \Leftrightarrow ~~~ \forall j, j \geqslant i: ~ s_j \models f</math> | ||
| + | ** <math>\Diamond</math> (<>) — в конце концов, т.е. <math>s_j \models \Diamond f ~~~ \Leftrightarrow ~~~ \exists j, j \geqslant i: ~ s_j \models f</math> | ||
| + | ** <math>X</math> (X) — в следующем состоянии, т.е. <math>s_j \models X f ~~~ \Leftrightarrow ~~~ i: ~ s_{j+1} \models f</math> | ||
| + | ** <math>\neg</math> (!) — логическое отрицание | ||
| + | * бинарные | ||
| + | ** <math>\wedge</math> (&&) — логическое И | ||
| + | ** <math>\vee</math> (||) — логическое ИЛИ | ||
| + | ** <math>\rightarrow</math> (->) — логическая импликация | ||
| + | ** <math>\leftrightarrow</math> (<->) — логическая эквивалентность | ||
| + | ** <math>U</math> (U) — до тех пор, пока (until) | ||
| + | |||
| + | ====Выполнимость формул:==== | ||
| + | * Задаётся последовательность состояний прохода <math>\sigma: s_0, s_1, s_2, \dots</math> | ||
| + | * <math>\forall i, i \geqslant 0, ~ \forall p </math> определена выполнимость <math> p </math> в <math> s_i </math> | ||
| + | * Семантика LTL: | ||
| + | ** <math>\sigma \models f \Leftrightarrow s_0 \models f</math> | ||
| + | ** <math>s_i \models \Box f \Leftrightarrow \forall j, j \geqslant i: s_j \models f</math> | ||
| + | ** <math>s_i \models \Diamond f \Leftrightarrow \exists j, j \geqslant i: s_j \models f</math> | ||
| + | ** <math>s_i \models Xf \Leftrightarrow s_{i+1} \models f </math> | ||
| + | ** '''Слабый Until:''' | ||
| + | *** всегда e, до тех пор, пока не f, при этом не факт, что f наступает (тогда всегда e) | ||
| + | *** <math>s_i \models e W f ~~ \Leftrightarrow ~~ s_i \models f \vee (s_i \models e \wedge s_{i+1} \models e W f)</math> | ||
| + | ** '''Сильный Until:''' | ||
| + | *** всегда e, до тех пор, пока не f, при этом f обязательно должно наступить | ||
| + | *** <math>s_i \models e U f ~~ \Leftrightarrow ~~ \begin{cases} | ||
| + | \exists j, j \geqslant i: ~ s_j \models f \\ | ||
| + | \forall k, i \leqslant k < j: ~ s_k \models e | ||
| + | \end{cases}</math> | ||
| + | |||
=== Логика LTL. Основные типы свойств LTL. Цикличность, стабильность, инвариант, гарантия, отклик, приоритет, корреляция. === | === Логика LTL. Основные типы свойств LTL. Цикличность, стабильность, инвариант, гарантия, отклик, приоритет, корреляция. === | ||
| + | '' Лекция 6, Слайды 38-39 '' | ||
| + | |||
| + | {| | ||
| + | |+ Распространенные LTL-формулы | ||
| + | |- | ||
| + | ! Формула !! Описание !! Тип || | ||
| + | |- | ||
| + | | <math>\Box p</math> || всегда p || ''инвариант'' || | ||
| + | |- | ||
| + | | <math>\diamond p</math> || рано или поздно p || ''гарантия'' || | ||
| + | |- | ||
| + | | <math>p \rightarrow \diamond q</math> || если p, то рано или поздно q || ''отклик'' || | ||
| + | |- | ||
| + | | <math>p \rightarrow q U r</math> | ||
| + | | если p то затем постоянно q до тех пор, | ||
| + | пока рано или поздно не наступит r | ||
| + | | ''приоритет'' | ||
| + | |- | ||
| + | | <math>\Box\diamond p</math> || всегда рано или позндно будет p || ''цикличность (прогресс)'' || | ||
| + | |- | ||
| + | | <math>\diamond\Box p</math> || рано или позндно всегда будет p || ''стабильность (бездействие)'' || | ||
| + | |- | ||
| + | | <math>\diamond p \rightarrow \diamond q</math> || если рано или поздно p, то рано или поздно q || ''корреляция'' || | ||
| + | |} | ||
| + | |||
=== Логика LTL. Эквивалентные преобразования формул LTL. === | === Логика LTL. Эквивалентные преобразования формул LTL. === | ||
| + | '' Лекция 6, Слайды 40 '' | ||
| + | {| width="100%" | ||
| + | | | ||
| + | <math> | ||
| + | \begin{align} | ||
| + | |||
| + | \neg\Box p & \Leftrightarrow & \diamond \neg p \\ | ||
| + | \neg\diamond p & \Leftrightarrow & \Box \neg p \\ | ||
| + | & & \\ | ||
| + | \neg(p U q) & \Leftrightarrow & \neg q \cup (\neg p \wedge \neg q) \\ | ||
| + | \neg(p \cup q) & \Leftrightarrow & \neg q U (\neg p \wedge \neg q) \\ | ||
| + | & & \\ | ||
| + | \Box (p \wedge q) & \Leftrightarrow & \Box p \wedge \Box q \\ | ||
| + | \diamond (p \vee q) & \Leftrightarrow & \diamond p \vee \diamond q \\ | ||
| + | \end{align} | ||
| + | </math> | ||
| + | | | ||
| + | <math> | ||
| + | \begin{align} | ||
| + | |||
| + | p \cup (q \vee r) & \Leftrightarrow & (p \cup q) \vee (p \cup r) \\ | ||
| + | (p \wedge q) \cup r & \Leftrightarrow & (p \cup r) \wedge (q \cup r) \\ | ||
| + | & & \\ | ||
| + | p U (q \vee r) & \Leftrightarrow & (p U q) \vee (p U r) \\ | ||
| + | (p U q) \cup r & \Leftrightarrow & (p U r) \wedge (q U r) \\ | ||
| + | & & \\ | ||
| + | \Box\diamond (p \wedge q) & \Leftrightarrow & \Box\diamond p \wedge \Box\diamond q \\ | ||
| + | \diamond\Box (p \vee q) & \Leftrightarrow & \diamond\Box p \vee \diamond\Box q \\ | ||
| + | |||
| + | |||
| + | \end{align} | ||
| + | </math> | ||
| + | |} | ||
| + | |||
=== Логика LTL. Оператор neXt. Свойства, инвариантные к прореживанию. === | === Логика LTL. Оператор neXt. Свойства, инвариантные к прореживанию. === | ||
| + | ''Лекция 7, слайды 22-25 '' | ||
| + | |||
| + | '''Оператор <math>X</math> нужно использовать аккуратно:''' | ||
| + | * с его помощью делается утверждение о выполнимости формулы на непосредственных потомках текущего состояния, | ||
| + | * в распределённых системах значение оператора <math>X</math> неочевидно, | ||
| + | * поскольку алгоритм планирования процессов неизвестен, не стоит формулировать спецификацию в предположении о том, | ||
| + | какое состояние будет следующим, | ||
| + | * стоит ограничиться предположением о справедливости планирования. | ||
| + | |||
| + | |||
| + | '''Свойства, инвариантные к прореживанию''' | ||
| + | * Пусть f – трасса некоторого вычисления над пропозициональными формулами P, | ||
| + | ** по трассе можно определить, выполняется ли на ней темпоральная формула, | ||
| + | ** трассу можно записать в форме: | ||
| + | ***<math>f^{n_1}, f^{n_2},f^{n_3}, ... </math> -- где значения пропозициональных формул на каждом интервале совпадают. | ||
| + | * Обозначим E(f) набор всех трасс, отличающихся лишь значениями <math>n_1, n_2, n_3</math> (т.е. длиной интервалов). | ||
| + | ** E(f) называется расширением прореживания f. | ||
| + | |||
| + | * Свойство f, инвариантное к прореживанию, либо истинно для всех трасс из <math>E(\psi)</math>, либо ни для одной из них: | ||
| + | ** <math>\psi \models f ~ \Rightarrow ~ \forall v \in E(\psi), v \models f </math> | ||
| + | * истинность такого свойства не зависит от длины трассы, а только от порядка, в котором пропозициональные формулы меняют свои значения; | ||
| + | * Теорема: все формулы LTL без оператора <math>X</math> инвариантны к прореживанию. | ||
| + | * в рамках LTL без <math>X</math> можно описать все свойства, инвариантные к прореживанию | ||
| + | |||
=== Логика LTL. Проверка выполнимости формул LTL при помощи автоматов Бюхи. Проверка LTL-формул в Spin. === | === Логика LTL. Проверка выполнимости формул LTL при помощи автоматов Бюхи. Проверка LTL-формул в Spin. === | ||
| + | '' Лекция 7, слайды 26-40 '' | ||
| + | |||
| + | '''Связь LTL с автоматами Бюхи''' | ||
| + | * Удобно проверять допустимость трасс для некоторого автомата Бюхи; | ||
| + | * Удобно описывать свойства правильности при помощи темпоральных формул; | ||
| + | * Для всякой LTL-формулы f существует автомат Бюхи, который допускает те и только те прогоны, которым соответствуют трассы, на которых выполнима f; | ||
| + | |||
| + | '''Переход от LTL к автоматам''' | ||
| + | * Привести свойство правильности LTL к форме never языка Promela достаточно просто: нужно построить отрицание LTL формулы и поместить его в тело never: | ||
| + | ** f выполняется на всех вычислениях <=> | ||
| + | ** !f не выполняется ни на одном вычислении <=> | ||
| + | ** автомат never {!f} не допускает ни одного прогона, полученного в результате синхронного выполнения с системой | ||
| + | |||
=== Логика LTL. Выразительная мощность LTL. Логики LTL + существование, CTL* и CTL. Сравнение выразительной мощности. === | === Логика LTL. Выразительная мощность LTL. Логики LTL + существование, CTL* и CTL. Сравнение выразительной мощности. === | ||
| + | При помощи конструкции never можно описать любой ω-регулярный автомат над словами | ||
| + | |||
| + | '''Выразительная мощность LTL''' | ||
| + | |||
| + | по сравнению с конструкциями never | ||
| + | |||
| + | * LTL описывает подмножество этого языка: | ||
| + | ** всё, выразимое на LTL, может быть описано при помощи never, | ||
| + | ** при помощи never можно описать свойства, не выразимые на LTL | ||
| + | * Добавление одного квантора существования над одним пропозициональным символом расширяет выразительные способности LTL до всех омега-регулярных автоматов над словами. | ||
| + | |||
| + | (p) может быть истинным после выполнения системой чётного количества шагов, но никогда не истинно после нечётного. | ||
| + | |||
| + | <math>\exists </math> t(t && [](t -> X!t) && [](!t -> Xt) && [](!t -> !p)) | ||
| + | |||
| + | LTL-формула описывает свойство, которое должно выполняться на '''всех''' вычислениях, начинающихся из исходного остояния системы | ||
| + | |||
| + | '''Логика СTL*''' | ||
| + | * Логика ветвящегося времени: | ||
| + | ** использует кванторы ∀ и ∃ для обозначения трасс, на которых может выполняться свойство | ||
| + | ** использует F вместо <> и G вместо [] | ||
| + | |||
| + | '''Логика СTL''' | ||
| + | |||
| + | Логика CTL – фрагмент логики CTL*, в котором кванторы могут встречаться только парами, причём в паре должны обязательно находиться один временной и один пространственный кванторы. Например: AG EF(p), A(p U q). | ||
| + | '''Выразительные возможности CTL* и CTL''' | ||
| + | * CTL* и CTL описывают подмножества w-регулярных автоматов над деревьями | ||
| + | ** автоматы над деревьями более выразительны, чем автоматы над словами (CTL-формула выполнима на дереве трасс, а не на одной трассе); | ||
| + | * CTL и LTL являются подмножествами CTL*; | ||
| + | * CTL и LTL не сравнимы по выразительной мощности (пересекаются, но не включают); | ||
| + | * на LTL можно описать свойства, не выразимые на CTL: | ||
| + | ** CTL не позволяет описать свойства вида []<>(p), | ||
| + | ** при помощи []<>(p) в LTL задаются ограничения справедливости; | ||
| + | * на CTL можно описать свойства, не выразимые на LTL: | ||
| + | ** на LTL нельзя описать свойства вида AGEF(p), | ||
| + | ** AGEF(p) используется для описания свойства reset: из любого состояния | ||
| + | система может перейти в нормальное | ||
== Верификация программ на моделях == | == Верификация программ на моделях == | ||
| Строка 283: | Строка 745: | ||
<u>Методы верификации:</u> | <u>Методы верификации:</u> | ||
| - | * "Полное" тестирование (слайды 14-22) | + | * "Полное" тестирование (''Лекция 1, слайды 14-22'') |
| - | * Имитационное моделирование | + | * Имитационное моделирование ([http://ru.wikipedia.org/wiki/Имитационное_моделирование вики]) |
| - | * Доказательство теорем (27-29) | + | * Доказательство теорем (''слайды 27-29'') |
| - | * Статический анализ (30-33) | + | * Статический анализ (''слайды 30-33'') |
| - | * Верификация на моделях (34-38) | + | * Верификация на моделях (''слайды 34-38'') |
<u>Типы программ:</u> | <u>Типы программ:</u> | ||
| Строка 304: | Строка 766: | ||
=== Подходы к верификации программ. Тестирование и имитационное моделирование. Область применения, плюсы и минусы. Проблема полноты тестового покрытия. === | === Подходы к верификации программ. Тестирование и имитационное моделирование. Область применения, плюсы и минусы. Проблема полноты тестового покрытия. === | ||
| + | «Тестирование может показать присутствие ошибок, но не может показать их отсутствия» © Дейкстра. | ||
| + | |||
| + | Обоснование полноты тестового покрытия: | ||
| + | * метод «чёрного ящика» (ЧЯ) — полное покрытие входных данных, | ||
| + | * метод «прозрачного ящика» (ПЯ) — полное покрытие кода программы. | ||
| + | Плюсы применения тестирования: | ||
| + | * проверяется та программа, которая будет использоваться, | ||
| + | * не требуется знание/использование дополнительных инструментальных средств, | ||
| + | * удобная локализация ошибки. | ||
| + | Минусы применения тестирования: | ||
| + | * не всегда есть условия для тестирования системы, | ||
| + | * проблема с воспроизводимостью тестов (частичное решение — имитационное моделирование). | ||
| + | |||
| + | ====Проблема полноты тестового покрытия==== | ||
| + | * Чёрный ящик: | ||
| + | ** для последовательных программ сложно перебрать все входные данные, | ||
| + | ** для параллельных программ — очень сложно, | ||
| + | ** для динамических структур данных, взаимодействия с окружением — невозможно. | ||
| + | * Прозрачный ящик: | ||
| + | ** большой размер покрытия, | ||
| + | ** часто невозможно построить 100% покрытие, | ||
| + | ** полное покрытие не гарантирует отсутствия ошибок. | ||
| + | Итоги: | ||
| + | * Полный перебор входных данных — невозможен. | ||
| + | * Полнота покрытия кода не гарантирует правильности. | ||
| + | * Ошибка — ошибочное вычисление системы. | ||
| + | * Полнота в терминах возможных вычислений — хороший критерий. | ||
=== Подходы к верификации программ. Доказательство теорем. Область применения, плюсы и минусы. === | === Подходы к верификации программ. Доказательство теорем. Область применения, плюсы и минусы. === | ||
| Строка 382: | Строка 871: | ||
=== Верификация на моделях. История развития верификации программ на моделях. Схема верификации программ на моделях. Классы проверяемых свойств правильности программы. === | === Верификация на моделях. История развития верификации программ на моделях. Схема верификации программ на моделях. Классы проверяемых свойств правильности программы. === | ||
| + | |||
| + | '' Лекция 1, Слайды 40-44 '' | ||
| + | |||
| + | '''История развития''' верификации программ на моделях: | ||
| + | * Флойд, 1967 – assertions, гипотеза о доказуемости корректности программы, | ||
| + | * Хоар, 1969 – пред- и пост-условия, триплеты Хоара (P | S | Q), логический вывод, | ||
| + | * Бойер, Мур, 1971 – первый автоматический прувер, | ||
| + | * Дейкстра, 1975 – Guarded Command Languages, | ||
| + | * Хоар, 1978 – взаимодействующие последовательные процессы (CSP). | ||
| + | * Пнуэли, 1977 – темпоральная логика LTL, | ||
| + | * Пнуэли, 1981 – логика ветвящегося времени (CTL), | ||
| + | * Кларк, Эмерсон, 1981 и Квили, Сифакис, 1982 – model checking (обход достижимых состояний), | ||
| + | * Варди и Вольпер, 1986 – новая техника model checking (анализ конформности), | ||
| + | * Хольцман, 1989 – верификатор SPIN. | ||
| + | * Бриан, 1989 – Двоичные решающие диаграммы (BDD), | ||
| + | * МакМиллан, 1993 – верификатор SMV (символьная верификация, BDD), | ||
| + | * Хольцман, Пелед, 1994 – редукция частичных порядков, | ||
| + | * 1995 – редукция частичных порядков в SPIN. | ||
| + | * Кларк, 1992 – абстракция для уменьшения числа состояний модели, | ||
| + | * Эльсаиди, 1994 – семантическая минимизация, | ||
| + | * Пелед, 1996, Бир, 1998 – верификация модели «на лету», | ||
| + | * Равви, 2000 – анализ достижимости с учётом спецификации, | ||
| + | * Эмерсон, Прасад, 1994 -- симметрия | ||
| + | '''Рост мощности''' model checking: | ||
| + | * 1992 год – 1020 состояний, | ||
| + | * 1994 год – 10120 состояний, | ||
| + | * 1998 год(?) – 10394 состояний | ||
| + | |||
| + | '' Лекция 2, Слайды 3-4 '' | ||
| + | |||
| + | ====Примеры классов свойств:==== | ||
| + | * Стандартные | ||
| + | ** Отсутствие ошибок времени выполнения (RTE), | ||
| + | ** Отсутствие удушения (starvation), | ||
| + | ** Не срабатывают ассерты(assertions). | ||
| + | ** [http://en.wikipedia.org/wiki/Deadlock deadlocks] ([http://ru.wikipedia.org/wiki/%D0%92%D0%B7%D0%B0%D0%B8%D0%BC%D0%BD%D0%B0%D1%8F_%D0%B1%D0%BB%D0%BE%D0%BA%D0%B8%D1%80%D0%BE%D0%B2%D0%BA%D0%B0 взаимная блокировка]) | ||
| + | ** [http://en.wikipedia.org/wiki/Race_condition Race condition] ([http://ru.wikipedia.org/wiki/%D0%A1%D0%BE%D1%81%D1%82%D0%BE%D1%8F%D0%BD%D0%B8%D0%B5_%D0%B3%D0%BE%D0%BD%D0%BA%D0%B8 состояние гонки]) | ||
| + | * Специфичные для конкретного приложения | ||
| + | ** требования справедливости | ||
| + | ** корректная завершаемость | ||
| + | ** причинно-следственный и темпоральный порядок состояний системы | ||
| + | ** Инварианты системы, | ||
| + | ** Индикаторы прогресса, | ||
| + | |||
| + | ====Схема верификации на модели==== | ||
| + | |||
| + | [[Изображение:Verif1.png|400px|Схема верификации на моделях (''Лекция 2, слайд 3'')]] | ||
| + | |||
=== Верификация при помощи Spin. Задание свойств состояний. === | === Верификация при помощи Spin. Задание свойств состояний. === | ||
'''Cвойства состояний''' | '''Cвойства состояний''' | ||
| Строка 390: | Строка 927: | ||
* метки терминальных состояний | * метки терминальных состояний | ||
** задаём допустимые точки останова процесса | ** задаём допустимые точки останова процесса | ||
| - | *** метка end | + | *** метка end -- система не может завершить работу без того, чтобы все активные процессы либо завершились, либо остановились в точках, помеченных метками end; |
=== Верификация при помощи Spin. Задание свойств последовательностей состояний. Циклы бездействия. Ограничения справедливости. === | === Верификация при помощи Spin. Задание свойств последовательностей состояний. Циклы бездействия. Ограничения справедливости. === | ||
| + | |||
| + | '''Свойства последовательностей состояний''' | ||
| + | * метки прогресса (чтобы найти циклы бездействия) | ||
| + | * утверждения о невозможности (never claims) | ||
| + | ** например, определяются LTL-формулами | ||
| + | * трассовые ассерты | ||
| + | |||
| + | '''Циклы бездействия'''. Мы хотим найти потенциально бесконечные циклы, не выполняющие никакой полезной работы. Помечаем меткой ''progress'' полезные операторы. Если найдется цикл, работающий потенциально бесконечно и не проходящий по метке progress, верификатор выдаст ошибку. | ||
| + | |||
| + | '''Ограничения справедливости'''. | ||
| + | Существует два основных варианта справедливости: | ||
| + | * слабая справедливость: | ||
| + | ** если оператор выполним бесконечно '''долго''', то он в конце концов будет выполнен | ||
| + | * сильная справедливость: | ||
| + | ** если оператор выполним бесконечно '''часто''', то он в конце концов будет выполнен. | ||
| + | Справедливость применима как к внутреннему, так и к | ||
| + | внешнему недетерминизму. | ||
| + | Использование сильной справедливости – существенно дороже слабой | ||
| + | |||
=== Верификация при помощи Spin. Задание свойств последовательностей состояний. Утверждения о невозможности. Трассовые ассерты. === | === Верификация при помощи Spin. Задание свойств последовательностей состояний. Утверждения о невозможности. Трассовые ассерты. === | ||
'''never claims (утверждения о невозможности):''' | '''never claims (утверждения о невозможности):''' | ||
| - | * выполняются синхронно с моделью | + | * выполняются синхронно с моделью |
| - | * если достигнут конец, то – ошибка | + | * если достигнут конец, то – ошибка |
| - | * состоят из выражений и конструкция задания | + | * состоят из выражений и конструкция задания потока управления |
| - | потока управления | + | * фактически, описывают распознающий автомат. |
| - | * фактически, описывают распознающий | + | |
| - | автомат. | + | |
'''Конструкция never''' | '''Конструкция never''' | ||
| Строка 413: | Строка 967: | ||
** завершена конструкция accept (допускающий цикл); | ** завершена конструкция accept (допускающий цикл); | ||
* бездействие может быть описано как конструкция never или её часть (для цикла бездействия есть тело never по умолчанию). | * бездействие может быть описано как конструкция never или её часть (для цикла бездействия есть тело never по умолчанию). | ||
| + | |||
| + | '''Видимость''' | ||
| + | * все конструкции never – глобальны; | ||
| + | * тем самым, в них можно ссылаться на | ||
| + | ** глобальные переменные, | ||
| + | ** каналы сообщений, | ||
| + | ** точки описания процессов (метки), | ||
| + | ** предопределённые глобальные переменные, | ||
| + | ** но не локальные переменные процессов; | ||
| + | |||
| + | '''Ассерты на трассы''' | ||
| + | Используются для описания выполнения правильных и неправильных последовательностей операторов send и recieve. ''Ассерт notrace'' - утверждает, что описанный шаблон поведения | ||
| + | невозможен. | ||
=== Верификация при помощи Spin. Принцип верификации нарушения свойств. Контрпримеры. Процесс верификации при помощи Spin. Использование LTL в Spin. === | === Верификация при помощи Spin. Принцип верификации нарушения свойств. Контрпримеры. Процесс верификации при помощи Spin. Использование LTL в Spin. === | ||
| + | * Свойство ''выполняется'' на модели, если оно выполняется на всех трассах. | ||
| + | * Свойство ''нарушается'' на модели, если нарушается хотя бы на одной из трасс. | ||
| + | * '''Принцип верификации нарушения свойств''' - проще проверять нарушение свойства, чем выполнение свойства. | ||
| + | ** Достаточно найти один контрпример | ||
| + | * Нарушение свойства описывается при помощи конструкции never – автомата, распознающего неправильное поведение | ||
| + | ** Автоматы Бюхи | ||
| + | * Свойства на последовательностях состояний удобно описывать при помощи темпоральной логики | ||
| + | ** Логика LTL | ||
| + | |||
| + | * <u>Связь LTL с автоматами Бюхи</u> | ||
| + | ** При помощи автомата Бюхи удобно проверять допустимость трасс. | ||
| + | ** При помощи темпоральных формул удобно описывать свойства правильности. | ||
| + | ** Для всякой LTL-формулы f существует автомат Бюхи, который допускает те и только те прогоны, которым соответствуют трассы, на которых выполнима f | ||
| + | * <u>Переход от LTL к автоматам</u> | ||
| + | ** f выполняется на всех вычислениях <=> | ||
| + | ** !f не выполняется ни на одном вычислении <=> | ||
| + | ** автомат never {!f} не допускает ни одного прогона, полученного в результате синхронного выполнения с системой | ||
| + | |||
| + | '''Использование LTL в Spin''' | ||
| + | * SPIN как раз и занимается тем, что преобразует LTL-формулы в автомат Бюхи, описываемый конструкцией never. | ||
| + | * Если во время верификации нашлась трасса, принадлежащая языку автомата Бюхи (т.е, конструкция never выполнилась, и мы дошли до её конца), SPIN выдаст '''контрпример''', содержащий эту трассу. | ||
== Система Spin и язык Promela == | == Система Spin и язык Promela == | ||
=== Система Spin. Процесс моделирования и верификации при помощи системы Spin. Конечность моделей на Promela. Асинхронное выполнение моделей. Недетерминированный поток управления. Понятие выполнимости оператора. === | === Система Spin. Процесс моделирования и верификации при помощи системы Spin. Конечность моделей на Promela. Асинхронное выполнение моделей. Недетерминированный поток управления. Понятие выполнимости оператора. === | ||
| + | |||
| + | |||
| + | '''Верификация программы на модели''' | ||
| + | * Мы хотим задавать, как система устроена и как она должна быть устроена | ||
| + | * Таким образом, нужно две нотации: | ||
| + | ** чтобы описать поведение (устройство системы) | ||
| + | ** чтобы описать требования (свойства правильности) | ||
| + | * Верификатор: | ||
| + | ** проверяет, что устройство системы удовлетворяет свойствам правильности | ||
| + | ** выбранная нотация гарантирует разрешимость проверки правильности любого свойства любой модели | ||
| + | * Все держится на трех китах | ||
| + | ** ''SPIN'' – Simple Promela Interpreter | ||
| + | *** верификация | ||
| + | *** моделирование | ||
| + | ** ''Promela'' – Process Meta Language - описание поведения модели | ||
| + | *** недетерминированный язык с охраняемыми командами | ||
| + | *** задача языка – разрешить описывать такие модели, которые могут быть верифицированы | ||
| + | ** ''LTL'' – Linear Temporal Logic - описание свойств | ||
| + | |||
| + | '''Конечность моделей на Promela''' | ||
| + | * У моделей – конечное число состояний (потенциально бесконечные элементы моделей в Promela ограничены) | ||
| + | ** гарантирует разрешимость верификации | ||
| + | * Почему число состояний конечно? | ||
| + | ** Число активных процессов конечно (от 0 до 255) | ||
| + | ** У каждого процесса – ограниченное количество операторов | ||
| + | ** Диапазоны типов данных ограничены | ||
| + | ** Размер всех каналов сообщений ограничен | ||
| + | |||
| + | '''Асинхронное выполнение моделей''' | ||
| + | * нет глобальных часов | ||
| + | * по умолчанию синхронизация отсутствует | ||
| + | |||
| + | '''Недетерминированный поток управления''' | ||
| + | * абстракция от деталей реализации | ||
| + | * Два уровня недетерминизма | ||
| + | ** внешний (выбор процесса) | ||
| + | *** процессы выполняются параллельно и асинхронно (между двумя последовательными операторами одного процесса может быть сколь угодно длинная пауза) | ||
| + | *** произвольная диспетчеризация процессов | ||
| + | *** выполнение операторов разных процессов происходит в произвольном порядке (основные операторы выполняются атомарно) | ||
| + | * внутренний (выбор действия в процессе). | ||
| + | ** в теле одного процесса также допускается недетерминированное ветвление | ||
| + | |||
| + | '''Понятие выполнимости оператора''' | ||
| + | * с любым оператором связаны понятия предусловия и эффекта | ||
| + | * оператор выполняется (производя эффект), только если предусловие истинно, в противном случае он заблокирован | ||
| + | ** Пример 1: ''q?m''; если канал ''q'' не пуст, читаем из него сообщение, иначе ждём | ||
| + | ** Пример 2: (''x > y) -> y++''; процесс будет заблокирован до тех пор, пока ''x'' не станет больше ''y''. После этого ''y'' увеличится на единицу. | ||
| + | |||
=== Язык Promela. Основные компоненты модели на языке Promela. Процессы, локальные и глобальные объекты данных, каналы сообщений. === | === Язык Promela. Основные компоненты модели на языке Promela. Процессы, локальные и глобальные объекты данных, каналы сообщений. === | ||
| + | |||
| + | '''Устройство модели'''. Существует три типа объектов: | ||
| + | * процессы | ||
| + | * глобальные и локальные объекты данных | ||
| + | * каналы сообщений | ||
| + | |||
| + | '''Процессы''' | ||
| + | * Поведение процесса задаётся в объявлении типа процесса (proctype) | ||
| + | * Экземпляр процесса – инстанциация proctype | ||
| + | * Два вида инстанцирования процессов: | ||
| + | ** В начальном состоянии системы - ''префикс active'' | ||
| + | ** В произвольном достижимом состоянии системы - ''оператор run'' | ||
| + | |||
| + | '''Локальные и глобальные объекты данных'''. Два уровня видимости: | ||
| + | * глобальный (данные видны всем активным процессам) | ||
| + | * локальный (данные видны только одному процессу) | ||
| + | ** есть особенность: локальная переменная, объявленная в теле процесса, видна во всем процессе (нет понятия ''область видимости переменной'' внутри процесса) | ||
| + | |||
| + | '''Каналы сообщений''' | ||
| + | * каналы бывают двух типов: | ||
| + | ** буферизованные (асинхронные) | ||
| + | ** небуферизованные (синхронные, рандеву) | ||
| + | * пример объявления канала: chan x = [10] of {int, short, bit}; | ||
| + | ** ''10'' - максимальное число сообщений в канале. 0 определяет канал рандеву. | ||
| + | ** ''{int, short, bit}'' - структура пересылаемых сообщений | ||
| + | |||
=== Язык Promela. Механизмы взаимодействия процессов в языке Promela. Глобальные переменные, каналы сообщений, явная синхронизация. === | === Язык Promela. Механизмы взаимодействия процессов в языке Promela. Глобальные переменные, каналы сообщений, явная синхронизация. === | ||
| + | |||
| + | ''см. предыдущий вопрос'' | ||
| + | |||
| + | '''Явная синхронизация:''' | ||
| + | |||
| + | active proctype A() provided (toggle == true){ | ||
| + | L: cnt++; | ||
| + | printf("A: cnt=%d\n", cnt); | ||
| + | toggle = false; | ||
| + | goto L | ||
| + | } | ||
| + | |||
| + | |||
| + | active proctype B() provided (toggle == false){ | ||
| + | L: cnt--; | ||
| + | printf("B: cnt=%d\n", cnt); | ||
| + | toggle = true; | ||
| + | goto L | ||
| + | } | ||
| + | |||
| + | Процесс выполняется, только если значение provided clause равно true. | ||
| + | По умолчанию значение равно true | ||
| + | |||
=== Язык Promela. Основные операторы языка Promela. Операторы-выражения, присваивания. === | === Язык Promela. Основные операторы языка Promela. Операторы-выражения, присваивания. === | ||
| + | '''Основные операторы языка Promela''' | ||
| + | * задают элементарные преобразования состояний, | ||
| + | * размечают дуги в системе переходов соответствующего процесса, | ||
| + | * их немного – всего 6 типов: | ||
| + | ** выражение | ||
| + | ** присваивание | ||
| + | ** печать | ||
| + | ** проверка свойства безопасности (assert) | ||
| + | ** отправка сообщения | ||
| + | ** прием сообщения | ||
| + | * оператор может быть: | ||
| + | ** выполнимым: ''может'' быть выполнен, | ||
| + | ** заблокированным: (пока что) ''не может'' быть выполнен, | ||
| + | ** выполнимость может зависеть от глобального состояния. | ||
| + | |||
| + | '''Оператор-выражение''' | ||
| + | * выполним только если выражение не равно 0 (истинно): | ||
| + | ** 2 < 3 – выполним всегда, | ||
| + | ** x < 27 – выполним только если значение x < 27, | ||
| + | ** 3 + х – выполним только если x != -3. | ||
| + | |||
| + | '''Оператор-присваивание''' | ||
| + | * всегда безусловно выполним, меняет значение только одной переменной, расположенной слева от “=”. | ||
| + | |||
=== Язык Promela. Основные операторы языка Promela. Отладочная печать, операторы skip, true, run, assert. === | === Язык Promela. Основные операторы языка Promela. Отладочная печать, операторы skip, true, run, assert. === | ||
| + | |||
| + | '''Основные операторы языка Promela''' | ||
| + | * присваивание: x++, x--, x = x + 1, x = run P(); | ||
| + | * выражение: (x), (1), run P(), skip, true, else, timeout; | ||
| + | * печать: printf(“x = %d\n”, x); | ||
| + | * ассерт: assert(1+1 == 2), assert(false); | ||
| + | * отправка сообщения: q!m; | ||
| + | * приём сообщения: q?m; | ||
| + | |||
| + | '''Отладочная печать''' | ||
| + | * оператор печати ''printf'', всегда безусловно выполним, на состояние не влияет | ||
| + | |||
| + | '''Псевдо-операторы''' | ||
| + | * skip: всегда выполним, без эффекта, эквивалент выражения (1), | ||
| + | * true: всегда выполним, без эффекта, эквивалент выражения (1), | ||
| + | * run: 0 если при создании процесса превышен лимит, pid в противном случае. | ||
| + | |||
| + | '''Оператор assert''' | ||
| + | * всегда выполнимо, не влияет на состояние системы, | ||
| + | * Spin сообщает об ошибке, если значение выражения равно 0 (false), | ||
| + | * используется для проверки свойств безопасности. | ||
| + | |||
=== Язык Promela. Чередование (интерливинг) операторов. Внешний и внутренний недетерминизм. Управление выполнимостью операторов. === | === Язык Promela. Чередование (интерливинг) операторов. Внешний и внутренний недетерминизм. Управление выполнимостью операторов. === | ||
| + | '''Чередование (интерливинг) операторов''' | ||
| + | * процессы выполняются параллельно и асинхронно, ''между двумя последовательными операторами одного процесса может быть сколь угодно длинная пауза'', | ||
| + | * произвольная диспетчеризация процессов, | ||
| + | * выполнение операторов разных процессов происходит в произвольном порядке, ''основные операторы выполняются атомарно'', | ||
| + | * в теле одного процесса также допускается недетерминированное ветвление | ||
| + | |||
| + | '''Внешний и внутренний недетерминизм''' | ||
| + | * два уровня недетерминизма: | ||
| + | ** внешний (выбор процесса), | ||
| + | ** внутренний (выбор действия в процессе). | ||
| + | |||
| + | '''Управление выполнимостью операторов''' | ||
| + | Основной инструмент управления выполнимостью операторов в Promela – выражения (expressions). | ||
| + | (a + b) -> c++; | ||
| + | Так же существуют управляющие конструкции if..fi и do..od | ||
| + | |||
=== Язык Promela. Задание потока управления последовательного процесса. Управляющие конструкции if, do. Организация внутреннего недетерминизма. === | === Язык Promela. Задание потока управления последовательного процесса. Управляющие конструкции if, do. Организация внутреннего недетерминизма. === | ||
| + | '''Задание потока управления последовательного процесса''' | ||
| + | 5 способов задать поток управления: | ||
| + | * последовательная композиция(“;”), метки, goto, | ||
| + | * структуризация (макросы и inline), | ||
| + | * атомарные последовательности (atomic, d_step), | ||
| + | * недетерминированный выбор и итерации (if..fi, do..od), | ||
| + | * escape-последовательности ({...}unless{...}). | ||
| + | |||
| + | '''Специальные выражения и переменные''' | ||
| + | * else – true, если ни один оператор процесса не выполним, | ||
| + | * timeout – true, если ни один оператор модели не выполним, | ||
| + | * _ – переменная, доступная только по записи, значение не сохраняет, | ||
| + | * _pid – минимальный доступный pid, | ||
| + | * _nr_pr – число активных процессов. | ||
| + | |||
=== Язык Promela. Каналы сообщений. Операторы отправки и приёма сообщений. Тип mtype. синхронная и асинхронная передача сообщений. === | === Язык Promela. Каналы сообщений. Операторы отправки и приёма сообщений. Тип mtype. синхронная и асинхронная передача сообщений. === | ||
| + | '''Каналы сообщений''' | ||
| + | * сообщения передаются через каналы (очереди/буфера ограниченного объёма) | ||
| + | * каналы бывают двух типов: | ||
| + | ** буферизованные (асинхронные), | ||
| + | ** небуферизованные (синхронные, рандеву); | ||
| + | |||
| + | chan x = [10] of {int, short, bit}; | ||
| + | |||
| + | '''Операторы отправки и приема сообщений''' | ||
| + | Отправка: ch!expr1,...exprn | ||
| + | * значения expri соответствуют типам в объявлении канала; | ||
| + | * выполнимо, если заданный канал не полон; | ||
| + | Приём: ch?const1 или var1,...constn или varn | ||
| + | * значения vari становятся равны соотв. значениям полей сообщения; | ||
| + | * значения consti ограничивают допустимые значения полей; | ||
| + | * выполнимо, если заданный канал не пуст и первое сообщение в канале соответствует всем константным значениям в операторе приёма сообщения; | ||
| + | |||
| + | '''Объявление mtype''' | ||
| + | * способ определить символьные константы (до 255) | ||
| + | |||
| + | Объявление mtype: | ||
| + | mtype = {foo, bar}; | ||
| + | mtype = {ack, msg, err, interrupt}; | ||
| + | |||
| + | Объявление переменных типа mtype: | ||
| + | mtype a; | ||
| + | mtype b = foo; | ||
| + | |||
| + | '''Cинхронная и асинхронная передача сообщений''' | ||
| + | * Асинхронная передача | ||
| + | ** асинхронные сообщения буферизуются для последующего приёма, пока канал не полон, | ||
| + | ** отправитель блокируется, когда канал полон, | ||
| + | ** получатель блокируется, когда канал пуст. | ||
| + | * Синхронная передача | ||
| + | ** ёмкость канала равна 0 - chan ch = [0] of {mtype}; | ||
| + | ** передача сообщений методом “рандеву”, | ||
| + | ** не хранит сообщения, | ||
| + | ** отправитель блокируется в ожидании получателя, и наоборот, | ||
| + | ** отправка и приём выполняются атомарно. | ||
| + | |||
=== Язык Promela. Каналы сообщений. Вспомогательные операции с каналами сообщений. === | === Язык Promela. Каналы сообщений. Вспомогательные операции с каналами сообщений. === | ||
| + | '''Другие операции с каналами''' | ||
| + | * len(q) – возвращает число сообщений в канале, | ||
| + | * empty(q) – возвращает true, если q пуст, | ||
| + | * full(q) – возвращает true, если q полон, | ||
| + | * nempty(q) – вместо !empty(q) (в целях оптимизации), | ||
| + | * nfull(q) – вместо !full(q) (в целях оптимизации). | ||
| + | * q?[n,m,p] | ||
| + | ** булевое выражение без побочных эффектов, | ||
| + | ** равно true только когда q?n,m,p выполнимо, однако не влияет на значения n,m,p и не меняет собержимое канала q; | ||
| + | * q?<n,m,p> | ||
| + | ** выполнимо тогда же, когда и q?n,m,p; влияет на значения n,m,p так же, как q?n,m,p, однако не меняет содержимое q; | ||
| + | * q?n(m,p) | ||
| + | ** вариант записи оператора приёма сообщения (т.е. q?n,m,p), | ||
| + | ** может использоваться для отделения переменной от констант | ||
| + | * q!!n,m,p – аналогично q!n,m,p, но сообщение n,m,p помещается в канал q сразу за первым сообщением, меньшим n,m,p; | ||
| + | * q??n,m,p – аналогично q?n,m,p, но из канала может быть выбрано любое сообщение (не обязательно первое). | ||
| + | |||
| + | ''Имя канала может быть локальным или глобальным, но канал сам по себе – всегда глобальный объект'' | ||
| + | |||
=== Язык Promela. Основные типы данных. Область видимости данных. === | === Язык Promela. Основные типы данных. Область видимости данных. === | ||
| + | |||
| + | {| | ||
| + | |+ Основные типы данных | ||
| + | ! Тип !! Диапазон !! Пример объявления !! | ||
| + | |- | ||
| + | | bit || 0..1 || bit turn = 1; || | ||
| + | |- | ||
| + | |bool || false..true || bool flag = true; || | ||
| + | |- | ||
| + | |byte || 0..255 || byte cnt; || | ||
| + | |- | ||
| + | |chan || 1..255 || chan q; || | ||
| + | |- | ||
| + | |mtype || 1..255 || mtype msg; || | ||
| + | |- | ||
| + | |pid || 1..255 || pid p; || | ||
| + | |- | ||
| + | |short || -2<sup>15</sup>..2<sup>15</sup>-1 || short s = 100; || | ||
| + | |- | ||
| + | |int || -2<sup>31</sup>..2<sup>31</sup>-1 || int x = 1; || | ||
| + | |- | ||
| + | |unsigned || 0..2<sup>n</sup>-1 || unsigned u : 3; // 3 бита [?] || | ||
| + | |} | ||
| + | |||
| + | * по умолчанию все объекты (и локальные и глобальные) инициализируются нулём; | ||
| + | * все переменные должны быть объявлены до первого использования; | ||
| + | * переменная может быть объявлена где угодно. | ||
| + | |||
| + | 'Одномерные массивы' | ||
| + | |||
| + | byte a[27]; | ||
| + | bit flags[4] = 1; | ||
| + | |||
| + | * все элементы массива инициализируются одним значением, | ||
| + | * индексы нумеруются с 0; | ||
| + | |||
| + | 'Пользовательские типы данных' | ||
| + | |||
| + | typedef record { | ||
| + | short f1; | ||
| + | byte f2 = 4; | ||
| + | } | ||
| + | record rr; | ||
| + | rr.f1 = 5; | ||
| + | |||
| + | '''Только два уровня видимости''' | ||
| + | * глобальный (данные видны всем активным процессам), | ||
| + | * локальный (данные видны только одному процессу) | ||
| + | ** подобластей (напр. для блоков) нет, | ||
| + | ** локальная переменная видна везде в теле процесса; | ||
| + | |||
| + | {{Курс ВПнМ}} | ||
Текущая версия
[править] Моделирование и абстракция
[править] Моделирование программ. Понятие состояния. Потенциальные и достижимые состояния. Требования к модели. Процесс построения модели.
Состояние программы - совокупность значений объектов данных и счётчика управления, связанных с некоторой моделью программы.
Модель - упрощённое описание реальности, выполненное с определенной целью.
- с каждым объектом может быть связано несколько моделей
- каждая модель отражает свой аспект реальности
Аспекты модели:
- простота - модель должна быть проще, чем реальность
- корректность - не расходиться с реальностью
- адекватность - соответствовать решаемой задаче
Построение модели
- формализация требований (постановка задачи моделирования)
- выбор языка моделирования
- абстракция системы до модели с учётом требований
Состояние называется достижимым, если существует вычисление программы, в котором оно присутствует
[править] Моделирование программ. Размеченные системы переходов. Детерминизм и недетерминизм. Вычисления и трассы. Свойства линейного времени. Выполнимость свойства на трассе.
Лекция 2, Слайды 39-50
[править] Размеченная система переходов (LTS)
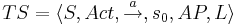
- S - множество состояний
- Act - множество действий
- τ - невидимое действие
-
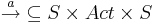 - тотальное отношение переходов. Тотальность означает, что из каждого состояния ведёт какое-то действие.
- тотальное отношение переходов. Тотальность означает, что из каждого состояния ведёт какое-то действие.
-
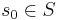 - начальное состояние, либо I - множество начальных состояний
- начальное состояние, либо I - множество начальных состояний
- AP - множество атомарных высказываний
-
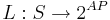 - функция разметки
- функция разметки
S, Act - конечные или счётные множества
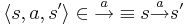
Пример LTS: Лекция 2, слайды 40-41
Прямые потомки
-
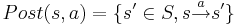 - такие состояния s', которые непосредственно вытекают из s через переход a
- такие состояния s', которые непосредственно вытекают из s через переход a
-
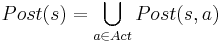 - все возможные состояния s', которые непосредственно вытекают из s
- все возможные состояния s', которые непосредственно вытекают из s
Система 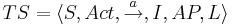 детерминирована:
детерминирована:
- по действиям тогда и только тогда, когда
-
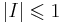
-
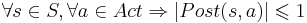 (количество потомков не больше одного)
(количество потомков не больше одного)
-
- по атомарным высказываниям
-
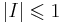
-
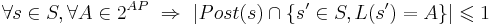 (количество одинаково размеченных потомков не больше одного)
(количество одинаково размеченных потомков не больше одного)
-
Недетерминизм - это фича! Полезен для:
- моделирования параллельного выполнения в режиме чередования (интерливинга)
- позволяет не указывать скорость выполнения процессов
- моделирования прототипа системы
- не ограничивает реализацию заданным порядком выполнения операторов
- построения абстракции реальной системы
- модель может быть построена по неполной информации
[править] Вычисления
- Конечный фрагмент вычисления σ системы переходов TS - это конечная последовательность чередующихся состояний и действий, заканчивающаяся состоянием:
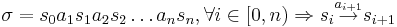
- Бесконечный (максимальный) фрагмент вычисления ρ -
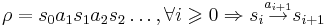
- Начальный фрагмент вычисления - фрагмент вычисления, для которого
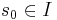
- Вычисление - начальный максимальный фрагмент вычисления (описывает последовательность состояний и действий)
Достижимое состояние (из начального) в системе переходов TS - такое состояние 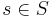 , для которого существует конечный фрагмент вычисления
, для которого существует конечный фрагмент вычисления 
Reach(TS) - множество всех достижимых состояний в TS
Трасса 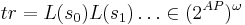 ;
; 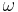 означает, что трасса может быть бесконечной
означает, что трасса может быть бесконечной
[править] Свойства линейного времени
- Свойство
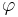 определяет набор допустимых трасс:
определяет набор допустимых трасс: 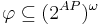
- Система переходов TS удовлетворяет свойству линейного времени
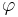 , если:
, если: 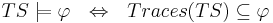
- по определению программа удовлетворяет свойству φ, если её система переходов удовлетворяет этому свойству:
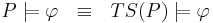 -
-
[править] Моделирование программ. Графы программ. Статическая и операционная семантика.
Граф программы – формальное описание текста программы.
- Dp -- единый абстрактный домен данных.
- P -- программа.
- Vp -- множество переменных программы(Var).
-
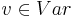
-
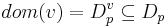 -- каждая переменная принадлежит какому-либо домену
-- каждая переменная принадлежит какому-либо домену
-
- n -- подстановка.
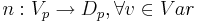
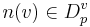
-
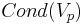 -- Набор булевых условий над Vp
-- Набор булевых условий над Vp
- формулы пропозициональной логики (
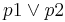 )
)
- условия на переменные вида
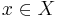 (p1: 3<=y<18, p2: f=4)
(p1: 3<=y<18, p2: f=4)
- формулы пропозициональной логики (
-
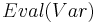 -- множество значений переменных. Собственно, это и есть подстановка.
-- множество значений переменных. Собственно, это и есть подстановка.
- Эффект операторов:
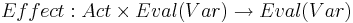
Граф программы:
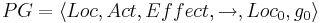
-
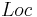 -- множество точек
-- множество точек
-
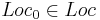 -- множество начальных точек
-- множество начальных точек
-
-
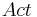 -- множество действий
-- множество действий
-
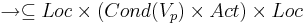 -- отношение перехода (Cond(Vp) -- это фактически страж оператора )
-- отношение перехода (Cond(Vp) -- это фактически страж оператора )
-
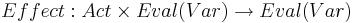 -- функция эффекта
-- функция эффекта
-
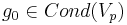 -- начальное условие
-- начальное условие
Получение TS из PG: раскрутка графа
- Состояние в TS -- это точка программы и текущая подстановка
- Начальное состояние -- исходная точка, удовлетворяющая начальному условию
- Атомарные высказывания в TS:
- находимся в точке программы l
- значение переменной x принадлежит некоторому множеству и это множество является подмножеством множеств значений этой переменной.
- Состояния
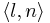 размечаются высказыванием о том, что мы находимся в точке программы
размечаются высказыванием о том, что мы находимся в точке программы 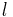 и всеми высказываниями, истинными в
и всеми высказываниями, истинными в 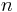
- Если в графе программы есть дуга из
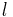 в
в 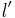 со стражем
со стражем 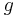 и действием
и действием 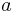 и в некоторой подстановке
и в некоторой подстановке 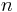 выполняется страж
выполняется страж 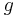 , то в системе переходов, которая соответствует этой программе будет присутствовать дуга из состояния
, то в системе переходов, которая соответствует этой программе будет присутствовать дуга из состояния 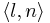 в состояние
в состояние 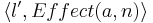 по действию
по действию 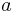 .
.
Системы переходов графов программ
Операционная семантика -- строгое описание того как из графа программы получить ее систему переходов. Описывается это все при помощи правил вывода.
TS(PG) -- система переходов графа программы 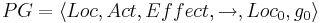 задается сигнатурой
задается сигнатурой 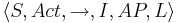
-
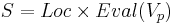 (декартово произведение точек программы на всевозможные подстановки)
(декартово произведение точек программы на всевозможные подстановки)
-
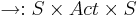 с соответствующим правилом вывода
с соответствующим правилом вывода 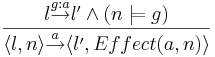
- Множество начальных состояний системы переходов описывается как множество состояний, в которых точка программы принадлежит начальным точкам, а на подстановках выполняется начальное условие графа программы:
-
- Множество атомарных высказываний -- это объединение множества точек программы и всевозможных булевых высказываний над переменными программы:
-
- Состояния вида
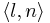 размечаются высказываниям о точке программы, в которой мы находимся и всеми высказываниями из множества всевозможных высказываний, которые верны в этой подстановке:
размечаются высказываниям о точке программы, в которой мы находимся и всеми высказываниями из множества всевозможных высказываний, которые верны в этой подстановке:
-
Пример: Лекция 4, слайд 16
Статическая и операционная семантика
Cтатическая семантика – набор ограничений, которым должна удовлетворять структура программы; Операционная семантика – понятие состояния программы и изменение состояния в ходе работы программы; то, как по графу строится LTS. (См. Л.5, сл. 15, 2010 )
[править] Параллелизм. Чередование систем переходов.
Лекция 4, слайды 21-24
- Действия независимых процессов чередуются.
- Порядок выполнения процессов не известен.
Чередование:
- эффект от параллельного выполнения независимых действий a и b равен эффекту от их последовательного выполнения в произвольном порядке:
-
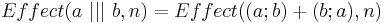
- ||| -- оператор чередования
- ; -- оператор последовательного выполнения
- + -- оператор недетерминированного выбора
-
Пример: Лекция 4, слайд 23
Чередование систем переходов
Пусть 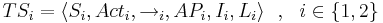
Тогда чередование этих систем 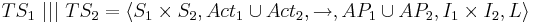 , где
, где
-
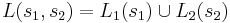
- оператор
 определяется как
определяется как
-
[править] Параллелизм. Чередование графов программ. Случаи без разделяемых переменных и с разделяемыми переменными.
Лекция 4, слайды 25—28
Для графов программ PG1 (над V1) и PG2 (над V2) без разделяемых переменных (т. е. 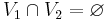 ):
):
- формула
 достоверно описывает параллельную композицию PG1 и PG2
достоверно описывает параллельную композицию PG1 и PG2
- в случае с разделяемыми переменными это не так (см. лекцию 4, слайд 26).
Пусть
Граф  над
над 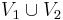 определяется так:
определяется так:
где отношение перехода  определяется следующими правилами вывода:
определяется следующими правилами вывода:
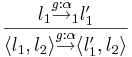 и
и 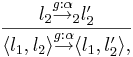
а 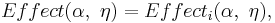 если
если 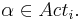
Пример: лекция 4, слайд 28. В указанном примере 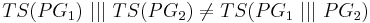
[править] Параллелизм. Синхронный параллелизм. Рандеву.
- распределённые программы выполняются параллельно
- в распределённой программе нет разделяемых переменных
Передача сообщений в распределённых программах:
- cинхронная передача сообщений (рандеву)
- асинхронная передача сообщений (каналы)
Синхронный обмен сообщениями:
- Процессы вместе выполняют синхронизированные действия
- Взаимодействие процессов - одновременно
Рандеву
-
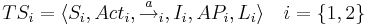
-
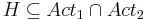 -- набор синхронизированных действий.
-- набор синхронизированных действий.
- действия из H должны быть синхронизированны
- действия не из H независимы и могут чередоваться
Тогда 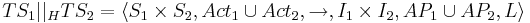 , где
, где
-
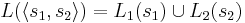
-
 определяется как:
определяется как:
- интерливинг для
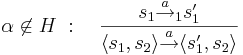 и
и 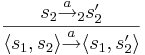
- рандеву для
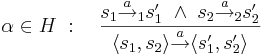
- интерливинг для
Пример рандеву: Лекция 4, слайд 32
Синхронный параллелизм
Тогда 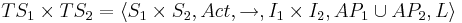 , где
, где
-
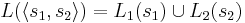
-
 определяется как:
определяется как: 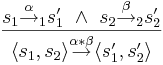
[править] Параллелизм. Асинхронный параллелизм. Системы с каналами. Операционная семантика.
Лекция 4. Слайды 36-39, 43-46
-
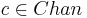 -- Процессы взаимодействуют с помощью каналов, представляющих собой FIFO буфера
-- Процессы взаимодействуют с помощью каналов, представляющих собой FIFO буфера
- dom(c) -- Каналы типизированы по передаваемым сообщениям
- cap(c) -- ёмкость канала. если cap(c) = 0, то взаимодействие сводится к рандеву
- действия по обмену сообщениями:
- c!v -- запись v в конец канала c. Выполняется только если буфер не полон ( < cap(c))
- c?x -- чтение в x из начала канала c. Выполняется только если буфер не пуст ( > cap(c))
- формально
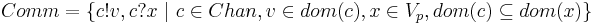
Системы с каналами.
- Граф программы PG над (Var,Chan) задаётся
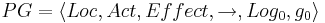 , где
, где 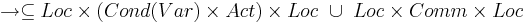
- Система с каналами CS над
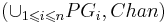 задаётся как
задаётся как ![CS = \left[PG_1 | PG_2 | \dots | PG_n\right]](/w/images/math/7/d/c/7dc0ccb31d277e9a4a9fcb406f008268.png) , где PGi — граф программы над (Vari,Chan)
, где PGi — граф программы над (Vari,Chan)
При асинхронной передаче сообщений (при cap(c) > 0):
- процесс Pi может выполнить
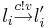 , только если в c хранится меньше cap(c) сообщений;
, только если в c хранится меньше cap(c) сообщений;
- процесс Pj может выполнить
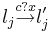 , только если c не пуст, после чего первый элемент v извлекается из c и присваивается x (атомарно).
, только если c не пуст, после чего первый элемент v извлекается из c и присваивается x (атомарно).
Оценка ξ значения канала c — это отображение канала на последовательность значений 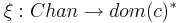 , такое что длина последовательности не превосходит ёмкости канала
, такое что длина последовательности не превосходит ёмкости канала 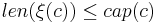 , и при этом
, и при этом 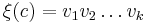 означает, что v1 — верхнее сообщение в буфере.
означает, что v1 — верхнее сообщение в буфере.
 = \left\{ \begin{array}{cc}
\xi(c'), & c \neq c' \\
v_1 v_2 \dots v_k, & c = c' \\
\end{array} \right.](/w/images/math/1/a/8/1a87c4fba48392f971a9805aca661eba.png) Кто понимает смысл этой хренотени, опишите, плз. Overrider 18:28, 22 мая 2009 (UTC)
Кто понимает смысл этой хренотени, опишите, плз. Overrider 18:28, 22 мая 2009 (UTC)
Исходная оценка 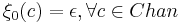
Операционная семантика: лекция 4, слайды 44—46
[править] операционная семантика
Пусть ![CS = \left[PG_1 | PG_2 | \dots | PG_n\right]](/w/images/math/7/d/c/7dc0ccb31d277e9a4a9fcb406f008268.png) – система с каналами над (Chan,Var), и
– система с каналами над (Chan,Var), и
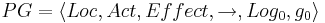
Система переходов TS(CS) описывается сигнатурой
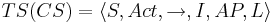 , где
, где
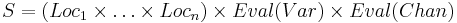
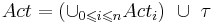
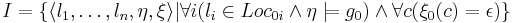
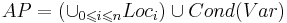
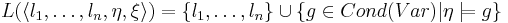
Правила вывода
-
интерливинг для
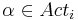
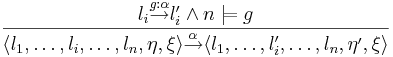
-
Синхронная передача сообщений через
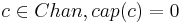
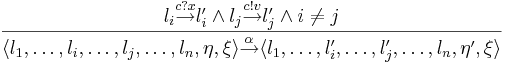
-
Асинхронная передача сообщений через
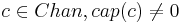
-
получить значение по каналу c и присвоить переменной x:
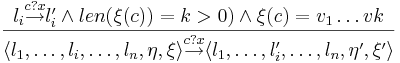 ,
,
где
![\eta' = \eta[x=v_1], \xi'=\xi[c=v_2 \dots v_k ]](/w/images/math/5/4/e/54eaf83ab73d022aab05c65bdc1fb18e.png)
-
передать значение
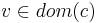 по каналу c:
по каналу c:
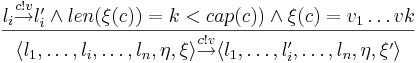 ,
,
где
![\xi'=\xi[c=v_1 \dots v_k v ]](/w/images/math/5/c/5/5c5e0c6afa281b6be0bef2a5e3ebb954.png)
-
[править] Абстракция. Абстракция трасс. Абстракция системы переходов. Необходимое и достаточное условие корректности LTS модели.
Представим трассу в форме интерпретации I: 
-
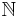 - множество натуральных чисел
- множество натуральных чисел
-
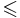 - отношение порядка на
- отношение порядка на 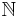
-
 (для каждого порядкового номера говорит истенен или ложен заданный на нем предикат)
(для каждого порядкового номера говорит истенен или ложен заданный на нем предикат)
Рассмотрим трассы tr и tr' такие, что
Будем говорить, что трасса tr' является абстракцией трассы tr (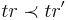 ), если
), если
-
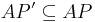
-
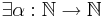 такое, что
такое, что
- α - неубывающая функция:
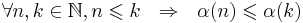
-

- α - неубывающая функция:
Пример абстракции трассы: Лекция 2, слайд 53
Определение. Пусть P – система, φ – произвольное свойство линейного времени. Корректной моделью P называется такая М, что:
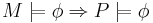 .
(позволяет проверять свойства программы на её модели )
.
(позволяет проверять свойства программы на её модели )
Необходимое и достаточное условие корректности модели:
Модель M системы P корректна тогда и только тогда, когда 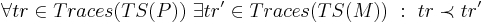 .
(для проверки такого условия нужно рассмотреть все трассы исходной системы, допускает, что в модели
больше состояний )
.
(для проверки такого условия нужно рассмотреть все трассы исходной системы, допускает, что в модели
больше состояний )
[править] Абстракция. Абстракция системы переходов. Достаточное условие корректности LTS модели. Адекватность LTS модели.
Абстракция системы переходов -- картинка на 4 слайде 3-й лекции.
Достаточное условие корректности LTS модели.
Пусть у нас имеются две системы переходов, TS1 и TS2 -- для системы и модели соответственно:
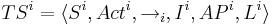
Достаточное условие корректности:
- Алфавит предикатов модели включен в алафвит предикатов системы:
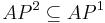
- Задано отображение
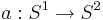 . На отображение накладываются следующие условия:
. На отображение накладываются следующие условия:
- Оно преобразует начальное состояние системы в начальное состояние модели:
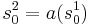
- Каждому переходу из системы должен соответствовать переход в модели:
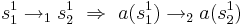
- Оно преобразует начальное состояние системы в начальное состояние модели:
- Метки на состояниях модели должны состоять только из предикатов модели:
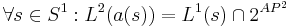
Модель называется адекватной, если:
- Атомарные высказывания, в терминах которых задаются свойства, присутствуют в разметке модели. (Необходимое условие)
- Из нарушения свойства на модели следует, что оно нарушается и на исходной системе. (Достаточное условие)
Необходимое условие адекватности модели свойствам правильности: алфавит предикатов свойств правильности включен в алфавит предикатов модели — 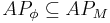 . Условие не является достаточным (см. примеры, лекция 3, слайды 4—5).
. Условие не является достаточным (см. примеры, лекция 3, слайды 4—5).
[править] Абстракция. Абстракция графов программ. Отношение слабой симуляции.
Лекция 10, слайды 8 - 11
Программа PG' корректно моделирует программу PG тогда и только тогда, когда система переходов TS(PG') корректно моделирует систему переходов TS(PG).
Будем говорить, что PG' моделирует PG, если
- в PG' присутствуют переменные, соответствующие наблюдаемым переменным PG
- все действия PG, влияющие на наблюдаемые переменные, отражены в модели (наблюдаемые операторы)
- модель корректно воспроизводит возможные последовательности изменения значений наблюдаемых переменных, присутствующих в PG
Отношение слабой симуляции не сохраняет количество шагов между состояниями. В связи с этим, не сохраняются свойства, не инвариантные к прореживанию (LTL: оператор neXt).
[править] Логика LTL, автоматы Бюхи
[править] Свойства правильности. Формулирование требований правильности программы. Двойственность. Типы свойств.
Лекция 5, слайды 2-14.
Требования правильности — утверждения о возможных и невозможных вариантах выполнения программы.
Двойственность :
- если какое-то утверждение невозможно, то обратное — неизбежно
- если какое-то утверждение неизбежно, то обратное — невозможно
- при помощи логики от одного можно переходить к другому при помощи отрицания
Способы описания свойств правильности:
- свойства достижимых состояний (свойства безопасности)
- свойства последовательности состояний (свойства живучести)
- в Promela:
- свойства состояний
- asserts:
- локальные ассерты процессов
- инварианты системы процессов
- метки терминальных состояний
- задаём допустимые точки останова прочесса
- asserts:
- свойства последовательностей состояний
- метки прогресса — чтобы найти циклы бездействия
- утверждения о невозможности (never claims) — например, LTL формулы
- трассовые ассерты — используются для описания правильных последовательностей выполнения операторов отправки и приема сообщения
- свойства состояний
[править] Свойства правильности. Свойства безопасности и живучести. Проверка таких свойств. Примеры свойств.
Типы свойств:
- свойства безопасности
- ничего плохого никогда не произойдет
- пример: инвариант системы (например, x всегда меньше y);
- задача верификатора -- найти те вычисления, которые ведут к нарушению безопасности.
- свойства живучести
- рано или поздно произойдет что-то хорошее
- пример: “отзывчивость” (например, если отправлен запрос, то рано или поздно будет сгенерирован ответ)
- задача верификатора – найти вычисления, в которых это “хорошее” может откладываться до бесконечности.
ps. автор терминов – Лесли Лампорт; см. Лекция 5, слайд 4.
[править] Автоматы Бюхи. Конечные автоматы. Проход автомата. Язык автомата.
Лекция 6, слайды 8 - 15
Конечный автомат
описывается сигнатурой: 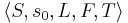 , где
, где
- S -- множество сотояний
-
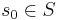 -- множество начальных состояний
-- множество начальных состояний
- L -- конечное множество меток
-
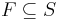 -- множество терминальных состояний
-- множество терминальных состояний
-
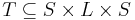 -- отношение перехода на состояниях
-- отношение перехода на состояниях
Детерминизм и недетерминизм
Конечный автомат называется детерминированным, если по метке и исходному состоянию можно однозначно определить целевое состояние:
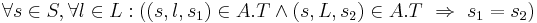
В противном случае автомат называется недетерминированным.
Проходом a конечного автомата 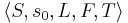 называется такое упорядоченное и, возможно, бесконечное множеств переходов из T:
называется такое упорядоченное и, возможно, бесконечное множеств переходов из T:
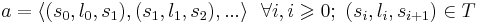
Допускающим проходом конечного автомата A называется конечный проход a, финальный переход которого
(sn − 1,ln − 1,sn) ведёт в терминальное состояние.
Языком автомата A называется множество слов в алфавите A.L, соответствующих допускающим проходам автомата А
[править] Автоматы Бюхи. Омега-допускание. Расширение автоматов Бюхи.
Лекция 6, слайды 19-20
Для любого бесконечного прохода σ конечного автомата А можно выделить два последовательных отрезка проходов:
- σ + -- конечный отрезок прохода σ, включающий в себя множество состояний, встречающихся конечное число раз
- σω -- бесконечный хвост прохода σ, включающий в себя множество состояний, встречающихся бесконечное число раз
Допускающий проход по Бюхи (ω-допускание) конечного автомата A называется такой бесконечный проход, в котором по крайней мере одно терминальное состояние встречается бесконечное число раз: 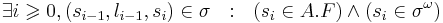
Расширение автоматов Бюхи.
- добавляем алфавит автомата меткой
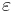
- все конечные проходы расширяем до бесконечности меткой
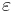
Примечание. При помощи автоматов Бюхи удобно проверять свойства живучести.
[править] Логика LTL. Синтаксис LTL. Семантика выполнимости формул. Сильный и слабый until.
Лекция 6, слайды 30 - 35
Особенности LTL:
- может использоваться для описания свойств как живучести, так и безопасности
- описывает свойства, которым должны удовлетворять линейные последовательности наблюдаемых состояний - трассы
- семантика LTL определена на бесконечных автоматах Бюхи. Для конечных проходов необходимо использовать расширение автомата.
Формула в LTL f::=
- p, q, ... — свойства состояний, включая true и false
- (f) — группировка при помощи скобок
-
 — унарные операторы
— унарные операторы
-
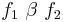 — бинарные операторы
— бинарные операторы
Операторы в LTL
- унарные
-
 ([]) — всегда в будущем, т.е.
([]) — всегда в будущем, т.е. 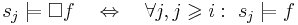
-
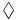 (<>) — в конце концов, т.е.
(<>) — в конце концов, т.е. 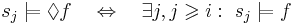
- X (X) — в следующем состоянии, т.е.
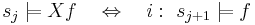
-
 (!) — логическое отрицание
(!) — логическое отрицание
-
- бинарные
-
 (&&) — логическое И
(&&) — логическое И
-
 (||) — логическое ИЛИ
(||) — логическое ИЛИ
-
 (->) — логическая импликация
(->) — логическая импликация
-
 (<->) — логическая эквивалентность
(<->) — логическая эквивалентность
- U (U) — до тех пор, пока (until)
-
[править] Выполнимость формул:
- Задаётся последовательность состояний прохода
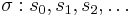
-
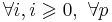 определена выполнимость p в si
определена выполнимость p в si
- Семантика LTL:
-

-
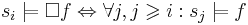
-
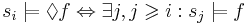
-
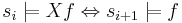
- Слабый Until:
- всегда e, до тех пор, пока не f, при этом не факт, что f наступает (тогда всегда e)
-
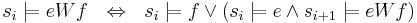
- Сильный Until:
- всегда e, до тех пор, пока не f, при этом f обязательно должно наступить
-
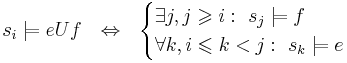
-
[править] Логика LTL. Основные типы свойств LTL. Цикличность, стабильность, инвариант, гарантия, отклик, приоритет, корреляция.
Лекция 6, Слайды 38-39
| Формула | Описание | Тип | |
|---|---|---|---|
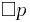 | всегда p | инвариант | |
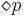 | рано или поздно p | гарантия | |
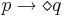 | если p, то рано или поздно q | отклик | |
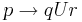
| если p то затем постоянно q до тех пор,
пока рано или поздно не наступит r | приоритет | |
 | всегда рано или позндно будет p | цикличность (прогресс) | |
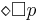 | рано или позндно всегда будет p | стабильность (бездействие) | |
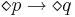 | если рано или поздно p, то рано или поздно q | корреляция |
[править] Логика LTL. Эквивалентные преобразования формул LTL.
Лекция 6, Слайды 40
|
|
|
[править] Логика LTL. Оператор neXt. Свойства, инвариантные к прореживанию.
Лекция 7, слайды 22-25
Оператор X нужно использовать аккуратно:
- с его помощью делается утверждение о выполнимости формулы на непосредственных потомках текущего состояния,
- в распределённых системах значение оператора X неочевидно,
- поскольку алгоритм планирования процессов неизвестен, не стоит формулировать спецификацию в предположении о том,
какое состояние будет следующим,
- стоит ограничиться предположением о справедливости планирования.
Свойства, инвариантные к прореживанию
- Пусть f – трасса некоторого вычисления над пропозициональными формулами P,
- по трассе можно определить, выполняется ли на ней темпоральная формула,
- трассу можно записать в форме:
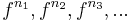 -- где значения пропозициональных формул на каждом интервале совпадают.
-- где значения пропозициональных формул на каждом интервале совпадают.
- Обозначим E(f) набор всех трасс, отличающихся лишь значениями n1,n2,n3 (т.е. длиной интервалов).
- E(f) называется расширением прореживания f.
- Свойство f, инвариантное к прореживанию, либо истинно для всех трасс из E(ψ), либо ни для одной из них:
-
- истинность такого свойства не зависит от длины трассы, а только от порядка, в котором пропозициональные формулы меняют свои значения;
- Теорема: все формулы LTL без оператора X инвариантны к прореживанию.
- в рамках LTL без X можно описать все свойства, инвариантные к прореживанию
[править] Логика LTL. Проверка выполнимости формул LTL при помощи автоматов Бюхи. Проверка LTL-формул в Spin.
Лекция 7, слайды 26-40
Связь LTL с автоматами Бюхи
- Удобно проверять допустимость трасс для некоторого автомата Бюхи;
- Удобно описывать свойства правильности при помощи темпоральных формул;
- Для всякой LTL-формулы f существует автомат Бюхи, который допускает те и только те прогоны, которым соответствуют трассы, на которых выполнима f;
Переход от LTL к автоматам
- Привести свойство правильности LTL к форме never языка Promela достаточно просто: нужно построить отрицание LTL формулы и поместить его в тело never:
- f выполняется на всех вычислениях <=>
- !f не выполняется ни на одном вычислении <=>
- автомат never {!f} не допускает ни одного прогона, полученного в результате синхронного выполнения с системой
[править] Логика LTL. Выразительная мощность LTL. Логики LTL + существование, CTL* и CTL. Сравнение выразительной мощности.
При помощи конструкции never можно описать любой ω-регулярный автомат над словами
Выразительная мощность LTL
по сравнению с конструкциями never
- LTL описывает подмножество этого языка:
- всё, выразимое на LTL, может быть описано при помощи never,
- при помощи never можно описать свойства, не выразимые на LTL
- Добавление одного квантора существования над одним пропозициональным символом расширяет выразительные способности LTL до всех омега-регулярных автоматов над словами.
(p) может быть истинным после выполнения системой чётного количества шагов, но никогда не истинно после нечётного.
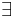 t(t && [](t -> X!t) && [](!t -> Xt) && [](!t -> !p))
t(t && [](t -> X!t) && [](!t -> Xt) && [](!t -> !p))
LTL-формула описывает свойство, которое должно выполняться на всех вычислениях, начинающихся из исходного остояния системы
Логика СTL*
- Логика ветвящегося времени:
- использует кванторы ∀ и ∃ для обозначения трасс, на которых может выполняться свойство
- использует F вместо <> и G вместо []
Логика СTL
Логика CTL – фрагмент логики CTL*, в котором кванторы могут встречаться только парами, причём в паре должны обязательно находиться один временной и один пространственный кванторы. Например: AG EF(p), A(p U q).
Выразительные возможности CTL* и CTL
- CTL* и CTL описывают подмножества w-регулярных автоматов над деревьями
- автоматы над деревьями более выразительны, чем автоматы над словами (CTL-формула выполнима на дереве трасс, а не на одной трассе);
- CTL и LTL являются подмножествами CTL*;
- CTL и LTL не сравнимы по выразительной мощности (пересекаются, но не включают);
- на LTL можно описать свойства, не выразимые на CTL:
- CTL не позволяет описать свойства вида []<>(p),
- при помощи []<>(p) в LTL задаются ограничения справедливости;
- на CTL можно описать свойства, не выразимые на LTL:
- на LTL нельзя описать свойства вида AGEF(p),
- AGEF(p) используется для описания свойства reset: из любого состояния
система может перейти в нормальное
[править] Верификация программ на моделях
[править] Задача проверки правильности программ. Валидация. Верификация. Системы с повышенными требованиями к надёжности. Реактивные программы. Параллельные программы. Особенности верификации таких программ.
Валидация - исследование и обоснование того, что спецификация ПО и само ПО через реализованную в нём функциональность удовлетворяет ребованиям пользователей.
Верификация - исследование и обоснование того, что программа соответствует своей спецификации.
Верификация в общем случае алгоритмически неразрешима.
Методы верификации:
- "Полное" тестирование (Лекция 1, слайды 14-22)
- Имитационное моделирование (вики)
- Доказательство теорем (слайды 27-29)
- Статический анализ (слайды 30-33)
- Верификация на моделях (слайды 34-38)
Типы программ:
- Традиционные программы
- завершимость
- спецификация включает в себя описание входа/выхода программы
- число состояний зависит от входных данных и переменных
- Реактивные программы
- работают в бесконечном цикле
- взаимодействуют с окружением
- спецификация представляет собой пары стимул/реакция
- Параллельные программы
- совместная работа нескольких компонент
- невоспроизводимость тестов
- ограниченные возможности по наблюдению
[править] Подходы к верификации программ. Тестирование и имитационное моделирование. Область применения, плюсы и минусы. Проблема полноты тестового покрытия.
«Тестирование может показать присутствие ошибок, но не может показать их отсутствия» © Дейкстра.
Обоснование полноты тестового покрытия:
- метод «чёрного ящика» (ЧЯ) — полное покрытие входных данных,
- метод «прозрачного ящика» (ПЯ) — полное покрытие кода программы.
Плюсы применения тестирования:
- проверяется та программа, которая будет использоваться,
- не требуется знание/использование дополнительных инструментальных средств,
- удобная локализация ошибки.
Минусы применения тестирования:
- не всегда есть условия для тестирования системы,
- проблема с воспроизводимостью тестов (частичное решение — имитационное моделирование).
[править] Проблема полноты тестового покрытия
- Чёрный ящик:
- для последовательных программ сложно перебрать все входные данные,
- для параллельных программ — очень сложно,
- для динамических структур данных, взаимодействия с окружением — невозможно.
- Прозрачный ящик:
- большой размер покрытия,
- часто невозможно построить 100% покрытие,
- полное покрытие не гарантирует отсутствия ошибок.
Итоги:
- Полный перебор входных данных — невозможен.
- Полнота покрытия кода не гарантирует правильности.
- Ошибка — ошибочное вычисление системы.
- Полнота в терминах возможных вычислений — хороший критерий.
[править] Подходы к верификации программ. Доказательство теорем. Область применения, плюсы и минусы.
Основные пункты:
- система и её свойста - формулы
- задан набор аксиом и правил вывода
- строится доказательство свойства-теоремы
- таким образом, производится качественный анализ системы
Пример: Лекция 1, слайд 28
Достоинства:
- работа с бесконечными пространствами состояний
- даёт более глубокое понимание системы
Недостатки
- медленная скорость работы
- может потребоваться помощь человека (построение инвариантов циклов)
- в общем случае нельзя построить полную систему аксиом и правил вывода
[править] Подходы к верификации программ. Статический анализ исходного кода программ. Область применения, плюсы и минусы.
Статистический анализ -- оцениваем для каждого состояния программы потенциально возможные значения переменных.
Пример: Лекция 1, Слайды 31-32
Особенности:
- анализ исходного текста без запуска программы
- в общем случае задача неразрешима
Достоинства:
- высокая скорость работы
- если ответ дан - ему можно верить
Недостатки:
- узкая область применения: компиляторы, анализ похожести кода, анализ безопасности
- ручная настройка при изменении применяемых свойств
[править] Подходы к верификации программ. Верификация программ на моделях. Процесс верификации программы при помощи её модели. Область применения, плюсы и минусы.
Лекция 1, Слайды 34-38 , 45
Особенности:
- проверка свойств на конечной модели
- исчерпывающий поиск по пространству состояний
- свойства задаются в терминах значений предикатов состояний программы или последовательности этих значений
Пример: Лекция 1, слайды 35-36
Процесс верификации программ на моделях:
- моделирование
- построение адекватной, корректной модели
- фильтрация "лишних" состояний
- спецификация свойств
- темпоральная логика
- полнота свойств
- верификация
- построение контр-примера
- анализ контр-примера
Достоинтсва:
- хорошая автоматизация
- если модель конечна, корректна и адекватна данному свойству, то будет получен точный ответ
- выявление редких ошибок
Недостатки:
- работает только для конечных моделей
Области применения
- сетевые и криптографические протоколы
- протоколы работы кэш-памяти
- интегральные схемы
- стандарты
- встроенные системы
- драйвера
- и прочие программы на C
[править] Верификация на моделях. История развития верификации программ на моделях. Схема верификации программ на моделях. Классы проверяемых свойств правильности программы.
Лекция 1, Слайды 40-44
История развития верификации программ на моделях:
- Флойд, 1967 – assertions, гипотеза о доказуемости корректности программы,
- Хоар, 1969 – пред- и пост-условия, триплеты Хоара (P | S | Q), логический вывод,
- Бойер, Мур, 1971 – первый автоматический прувер,
- Дейкстра, 1975 – Guarded Command Languages,
- Хоар, 1978 – взаимодействующие последовательные процессы (CSP).
- Пнуэли, 1977 – темпоральная логика LTL,
- Пнуэли, 1981 – логика ветвящегося времени (CTL),
- Кларк, Эмерсон, 1981 и Квили, Сифакис, 1982 – model checking (обход достижимых состояний),
- Варди и Вольпер, 1986 – новая техника model checking (анализ конформности),
- Хольцман, 1989 – верификатор SPIN.
- Бриан, 1989 – Двоичные решающие диаграммы (BDD),
- МакМиллан, 1993 – верификатор SMV (символьная верификация, BDD),
- Хольцман, Пелед, 1994 – редукция частичных порядков,
- 1995 – редукция частичных порядков в SPIN.
- Кларк, 1992 – абстракция для уменьшения числа состояний модели,
- Эльсаиди, 1994 – семантическая минимизация,
- Пелед, 1996, Бир, 1998 – верификация модели «на лету»,
- Равви, 2000 – анализ достижимости с учётом спецификации,
- Эмерсон, Прасад, 1994 -- симметрия
Рост мощности model checking:
- 1992 год – 1020 состояний,
- 1994 год – 10120 состояний,
- 1998 год(?) – 10394 состояний
Лекция 2, Слайды 3-4
[править] Примеры классов свойств:
- Стандартные
- Отсутствие ошибок времени выполнения (RTE),
- Отсутствие удушения (starvation),
- Не срабатывают ассерты(assertions).
- deadlocks (взаимная блокировка)
- Race condition (состояние гонки)
- Специфичные для конкретного приложения
- требования справедливости
- корректная завершаемость
- причинно-следственный и темпоральный порядок состояний системы
- Инварианты системы,
- Индикаторы прогресса,
[править] Схема верификации на модели
[править] Верификация при помощи Spin. Задание свойств состояний.
Cвойства состояний
- asserts
- локальные ассерты процессов
- инварианты системы процессов
- active proctype invariant() { assert(something)}
- метки терминальных состояний
- задаём допустимые точки останова процесса
- метка end -- система не может завершить работу без того, чтобы все активные процессы либо завершились, либо остановились в точках, помеченных метками end;
- задаём допустимые точки останова процесса
[править] Верификация при помощи Spin. Задание свойств последовательностей состояний. Циклы бездействия. Ограничения справедливости.
Свойства последовательностей состояний
- метки прогресса (чтобы найти циклы бездействия)
- утверждения о невозможности (never claims)
- например, определяются LTL-формулами
- трассовые ассерты
Циклы бездействия. Мы хотим найти потенциально бесконечные циклы, не выполняющие никакой полезной работы. Помечаем меткой progress полезные операторы. Если найдется цикл, работающий потенциально бесконечно и не проходящий по метке progress, верификатор выдаст ошибку.
Ограничения справедливости. Существует два основных варианта справедливости:
- слабая справедливость:
- если оператор выполним бесконечно долго, то он в конце концов будет выполнен
- сильная справедливость:
- если оператор выполним бесконечно часто, то он в конце концов будет выполнен.
Справедливость применима как к внутреннему, так и к внешнему недетерминизму. Использование сильной справедливости – существенно дороже слабой
[править] Верификация при помощи Spin. Задание свойств последовательностей состояний. Утверждения о невозможности. Трассовые ассерты.
never claims (утверждения о невозможности):
- выполняются синхронно с моделью
- если достигнут конец, то – ошибка
- состоят из выражений и конструкция задания потока управления
- фактически, описывают распознающий автомат.
Конструкция never
- может быть как детерминированной, так и нет;
- содержит только выражения без побочных эффектов (соотв. булевым высказываниям на состояниях);
- используются для описания неправильного поведения системы;
- прерывается при блокировании:
- блокируется => наблюдаемое поведение не соответствует описанному,
- паузы в выполнении тела never должны быть явно заданы как бесконечные циклы;
- never нарушается, если:
- достигнута закрывающая скобка,
- завершена конструкция accept (допускающий цикл);
- бездействие может быть описано как конструкция never или её часть (для цикла бездействия есть тело never по умолчанию).
Видимость
- все конструкции never – глобальны;
- тем самым, в них можно ссылаться на
- глобальные переменные,
- каналы сообщений,
- точки описания процессов (метки),
- предопределённые глобальные переменные,
- но не локальные переменные процессов;
Ассерты на трассы Используются для описания выполнения правильных и неправильных последовательностей операторов send и recieve. Ассерт notrace - утверждает, что описанный шаблон поведения невозможен.
[править] Верификация при помощи Spin. Принцип верификации нарушения свойств. Контрпримеры. Процесс верификации при помощи Spin. Использование LTL в Spin.
- Свойство выполняется на модели, если оно выполняется на всех трассах.
- Свойство нарушается на модели, если нарушается хотя бы на одной из трасс.
- Принцип верификации нарушения свойств - проще проверять нарушение свойства, чем выполнение свойства.
- Достаточно найти один контрпример
- Нарушение свойства описывается при помощи конструкции never – автомата, распознающего неправильное поведение
- Автоматы Бюхи
- Свойства на последовательностях состояний удобно описывать при помощи темпоральной логики
- Логика LTL
- Связь LTL с автоматами Бюхи
- При помощи автомата Бюхи удобно проверять допустимость трасс.
- При помощи темпоральных формул удобно описывать свойства правильности.
- Для всякой LTL-формулы f существует автомат Бюхи, который допускает те и только те прогоны, которым соответствуют трассы, на которых выполнима f
- Переход от LTL к автоматам
- f выполняется на всех вычислениях <=>
- !f не выполняется ни на одном вычислении <=>
- автомат never {!f} не допускает ни одного прогона, полученного в результате синхронного выполнения с системой
Использование LTL в Spin
- SPIN как раз и занимается тем, что преобразует LTL-формулы в автомат Бюхи, описываемый конструкцией never.
- Если во время верификации нашлась трасса, принадлежащая языку автомата Бюхи (т.е, конструкция never выполнилась, и мы дошли до её конца), SPIN выдаст контрпример, содержащий эту трассу.
[править] Система Spin и язык Promela
[править] Система Spin. Процесс моделирования и верификации при помощи системы Spin. Конечность моделей на Promela. Асинхронное выполнение моделей. Недетерминированный поток управления. Понятие выполнимости оператора.
Верификация программы на модели
- Мы хотим задавать, как система устроена и как она должна быть устроена
- Таким образом, нужно две нотации:
- чтобы описать поведение (устройство системы)
- чтобы описать требования (свойства правильности)
- Верификатор:
- проверяет, что устройство системы удовлетворяет свойствам правильности
- выбранная нотация гарантирует разрешимость проверки правильности любого свойства любой модели
- Все держится на трех китах
- SPIN – Simple Promela Interpreter
- верификация
- моделирование
- Promela – Process Meta Language - описание поведения модели
- недетерминированный язык с охраняемыми командами
- задача языка – разрешить описывать такие модели, которые могут быть верифицированы
- LTL – Linear Temporal Logic - описание свойств
- SPIN – Simple Promela Interpreter
Конечность моделей на Promela
- У моделей – конечное число состояний (потенциально бесконечные элементы моделей в Promela ограничены)
- гарантирует разрешимость верификации
- Почему число состояний конечно?
- Число активных процессов конечно (от 0 до 255)
- У каждого процесса – ограниченное количество операторов
- Диапазоны типов данных ограничены
- Размер всех каналов сообщений ограничен
Асинхронное выполнение моделей
- нет глобальных часов
- по умолчанию синхронизация отсутствует
Недетерминированный поток управления
- абстракция от деталей реализации
- Два уровня недетерминизма
- внешний (выбор процесса)
- процессы выполняются параллельно и асинхронно (между двумя последовательными операторами одного процесса может быть сколь угодно длинная пауза)
- произвольная диспетчеризация процессов
- выполнение операторов разных процессов происходит в произвольном порядке (основные операторы выполняются атомарно)
- внешний (выбор процесса)
- внутренний (выбор действия в процессе).
- в теле одного процесса также допускается недетерминированное ветвление
Понятие выполнимости оператора
- с любым оператором связаны понятия предусловия и эффекта
- оператор выполняется (производя эффект), только если предусловие истинно, в противном случае он заблокирован
- Пример 1: q?m; если канал q не пуст, читаем из него сообщение, иначе ждём
- Пример 2: (x > y) -> y++; процесс будет заблокирован до тех пор, пока x не станет больше y. После этого y увеличится на единицу.
[править] Язык Promela. Основные компоненты модели на языке Promela. Процессы, локальные и глобальные объекты данных, каналы сообщений.
Устройство модели. Существует три типа объектов:
- процессы
- глобальные и локальные объекты данных
- каналы сообщений
Процессы
- Поведение процесса задаётся в объявлении типа процесса (proctype)
- Экземпляр процесса – инстанциация proctype
- Два вида инстанцирования процессов:
- В начальном состоянии системы - префикс active
- В произвольном достижимом состоянии системы - оператор run
Локальные и глобальные объекты данных. Два уровня видимости:
- глобальный (данные видны всем активным процессам)
- локальный (данные видны только одному процессу)
- есть особенность: локальная переменная, объявленная в теле процесса, видна во всем процессе (нет понятия область видимости переменной внутри процесса)
Каналы сообщений
- каналы бывают двух типов:
- буферизованные (асинхронные)
- небуферизованные (синхронные, рандеву)
- пример объявления канала: chan x = [10] of {int, short, bit};
- 10 - максимальное число сообщений в канале. 0 определяет канал рандеву.
- {int, short, bit} - структура пересылаемых сообщений
[править] Язык Promela. Механизмы взаимодействия процессов в языке Promela. Глобальные переменные, каналы сообщений, явная синхронизация.
см. предыдущий вопрос
Явная синхронизация:
active proctype A() provided (toggle == true){
L: cnt++;
printf("A: cnt=%d\n", cnt);
toggle = false;
goto L
}
active proctype B() provided (toggle == false){
L: cnt--;
printf("B: cnt=%d\n", cnt);
toggle = true;
goto L
}
Процесс выполняется, только если значение provided clause равно true. По умолчанию значение равно true
[править] Язык Promela. Основные операторы языка Promela. Операторы-выражения, присваивания.
Основные операторы языка Promela
- задают элементарные преобразования состояний,
- размечают дуги в системе переходов соответствующего процесса,
- их немного – всего 6 типов:
- выражение
- присваивание
- печать
- проверка свойства безопасности (assert)
- отправка сообщения
- прием сообщения
- оператор может быть:
- выполнимым: может быть выполнен,
- заблокированным: (пока что) не может быть выполнен,
- выполнимость может зависеть от глобального состояния.
Оператор-выражение
- выполним только если выражение не равно 0 (истинно):
- 2 < 3 – выполним всегда,
- x < 27 – выполним только если значение x < 27,
- 3 + х – выполним только если x != -3.
Оператор-присваивание
- всегда безусловно выполним, меняет значение только одной переменной, расположенной слева от “=”.
[править] Язык Promela. Основные операторы языка Promela. Отладочная печать, операторы skip, true, run, assert.
Основные операторы языка Promela
- присваивание: x++, x--, x = x + 1, x = run P();
- выражение: (x), (1), run P(), skip, true, else, timeout;
- печать: printf(“x = %d\n”, x);
- ассерт: assert(1+1 == 2), assert(false);
- отправка сообщения: q!m;
- приём сообщения: q?m;
Отладочная печать
- оператор печати printf, всегда безусловно выполним, на состояние не влияет
Псевдо-операторы
- skip: всегда выполним, без эффекта, эквивалент выражения (1),
- true: всегда выполним, без эффекта, эквивалент выражения (1),
- run: 0 если при создании процесса превышен лимит, pid в противном случае.
Оператор assert
- всегда выполнимо, не влияет на состояние системы,
- Spin сообщает об ошибке, если значение выражения равно 0 (false),
- используется для проверки свойств безопасности.
[править] Язык Promela. Чередование (интерливинг) операторов. Внешний и внутренний недетерминизм. Управление выполнимостью операторов.
Чередование (интерливинг) операторов
- процессы выполняются параллельно и асинхронно, между двумя последовательными операторами одного процесса может быть сколь угодно длинная пауза,
- произвольная диспетчеризация процессов,
- выполнение операторов разных процессов происходит в произвольном порядке, основные операторы выполняются атомарно,
- в теле одного процесса также допускается недетерминированное ветвление
Внешний и внутренний недетерминизм
- два уровня недетерминизма:
- внешний (выбор процесса),
- внутренний (выбор действия в процессе).
Управление выполнимостью операторов Основной инструмент управления выполнимостью операторов в Promela – выражения (expressions). (a + b) -> c++; Так же существуют управляющие конструкции if..fi и do..od
[править] Язык Promela. Задание потока управления последовательного процесса. Управляющие конструкции if, do. Организация внутреннего недетерминизма.
Задание потока управления последовательного процесса 5 способов задать поток управления:
- последовательная композиция(“;”), метки, goto,
- структуризация (макросы и inline),
- атомарные последовательности (atomic, d_step),
- недетерминированный выбор и итерации (if..fi, do..od),
- escape-последовательности ({...}unless{...}).
Специальные выражения и переменные
- else – true, если ни один оператор процесса не выполним,
- timeout – true, если ни один оператор модели не выполним,
- _ – переменная, доступная только по записи, значение не сохраняет,
- _pid – минимальный доступный pid,
- _nr_pr – число активных процессов.
[править] Язык Promela. Каналы сообщений. Операторы отправки и приёма сообщений. Тип mtype. синхронная и асинхронная передача сообщений.
Каналы сообщений
- сообщения передаются через каналы (очереди/буфера ограниченного объёма)
- каналы бывают двух типов:
- буферизованные (асинхронные),
- небуферизованные (синхронные, рандеву);
chan x = [10] of {int, short, bit};
Операторы отправки и приема сообщений Отправка: ch!expr1,...exprn
- значения expri соответствуют типам в объявлении канала;
- выполнимо, если заданный канал не полон;
Приём: ch?const1 или var1,...constn или varn
- значения vari становятся равны соотв. значениям полей сообщения;
- значения consti ограничивают допустимые значения полей;
- выполнимо, если заданный канал не пуст и первое сообщение в канале соответствует всем константным значениям в операторе приёма сообщения;
Объявление mtype
- способ определить символьные константы (до 255)
Объявление mtype: mtype = {foo, bar}; mtype = {ack, msg, err, interrupt};
Объявление переменных типа mtype: mtype a; mtype b = foo;
Cинхронная и асинхронная передача сообщений
- Асинхронная передача
- асинхронные сообщения буферизуются для последующего приёма, пока канал не полон,
- отправитель блокируется, когда канал полон,
- получатель блокируется, когда канал пуст.
- Синхронная передача
- ёмкость канала равна 0 - chan ch = [0] of {mtype};
- передача сообщений методом “рандеву”,
- не хранит сообщения,
- отправитель блокируется в ожидании получателя, и наоборот,
- отправка и приём выполняются атомарно.
[править] Язык Promela. Каналы сообщений. Вспомогательные операции с каналами сообщений.
Другие операции с каналами
- len(q) – возвращает число сообщений в канале,
- empty(q) – возвращает true, если q пуст,
- full(q) – возвращает true, если q полон,
- nempty(q) – вместо !empty(q) (в целях оптимизации),
- nfull(q) – вместо !full(q) (в целях оптимизации).
- q?[n,m,p]
- булевое выражение без побочных эффектов,
- равно true только когда q?n,m,p выполнимо, однако не влияет на значения n,m,p и не меняет собержимое канала q;
- q?<n,m,p>
- выполнимо тогда же, когда и q?n,m,p; влияет на значения n,m,p так же, как q?n,m,p, однако не меняет содержимое q;
- q?n(m,p)
- вариант записи оператора приёма сообщения (т.е. q?n,m,p),
- может использоваться для отделения переменной от констант
- q!!n,m,p – аналогично q!n,m,p, но сообщение n,m,p помещается в канал q сразу за первым сообщением, меньшим n,m,p;
- q??n,m,p – аналогично q?n,m,p, но из канала может быть выбрано любое сообщение (не обязательно первое).
Имя канала может быть локальным или глобальным, но канал сам по себе – всегда глобальный объект
[править] Язык Promela. Основные типы данных. Область видимости данных.
| Тип | Диапазон | Пример объявления | |
|---|---|---|---|
| bit | 0..1 | bit turn = 1; | |
| bool | false..true | bool flag = true; | |
| byte | 0..255 | byte cnt; | |
| chan | 1..255 | chan q; | |
| mtype | 1..255 | mtype msg; | |
| pid | 1..255 | pid p; | |
| short | -215..215-1 | short s = 100; | |
| int | -231..231-1 | int x = 1; | |
| unsigned | 0..2n-1 | unsigned u : 3; // 3 бита [?] |
- по умолчанию все объекты (и локальные и глобальные) инициализируются нулём;
- все переменные должны быть объявлены до первого использования;
- переменная может быть объявлена где угодно.
'Одномерные массивы'
byte a[27]; bit flags[4] = 1;
- все элементы массива инициализируются одним значением,
- индексы нумеруются с 0;
'Пользовательские типы данных'
typedef record { short f1; byte f2 = 4; } record rr; rr.f1 = 5;
Только два уровня видимости
- глобальный (данные видны всем активным процессам),
- локальный (данные видны только одному процессу)
- подобластей (напр. для блоков) нет,
- локальная переменная видна везде в теле процесса;