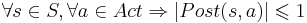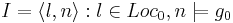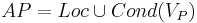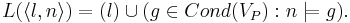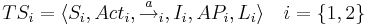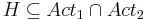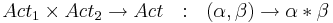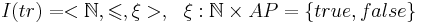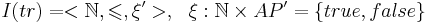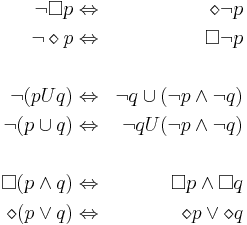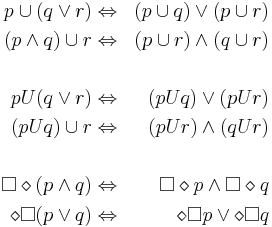ВПнМ/Теормин

Материал из eSyr's wiki.

(Различия между версиями)

Перейти к: навигация, поиск

Версия 12:12, 21 мая 2009

Содержание

1 Моделирование и абстракция
2 Логика LTL, автоматы Бюхи
3 Верификация программ на моделях
4 Система Spin и язык Promela

Моделирование и абстракция

Моделирование программ. Понятие состояния. Потенциальные и достижимые состояния. Требования к модели. Процесс построения модели.

Схема верификации на моделях (Лекция 2, слайд 3)

Состояние программы - совокупность значений переменных и управления, связанных с некоторой моделью программы.

Модель - упрощённое описание реальности, выполненное с определенной целью.

с каждым объектом может быть связано несколько моделей
каждая модель отражает свой аспект реальности

Аспекты модели:

простота - модель должна быть проще, чем реальность
корректность - не расходиться с реальностью
адекватность - соответствовать решаемой задаче

Построение модели

формализация требований (постановка задачи моделирования)
выбор языка моделирования
абстракция системы до модели с учётом требований

Моделирование программ. Размеченные системы переходов. Детерминизм и недетерминизм. Вычисления и трассы. Свойства линейного времени. Выполнимость свойства на трассе.

Лекция 2, Слайды 39-50

Размеченная система переходов (LTS)

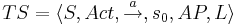
$TS = \langle S, Act, \overset{a}{\rightarrow} ,s_0, AP, L \rangle$

S - множество состояний
Act - множество действий
$τ$ - невидимое действие
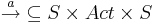$\overset{a}{\rightarrow} \subseteq S \times Act \times S$ - тотальное отношение переходов
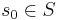$s_0 \in S$ - начальное состояние
AP - множество атомарных высказываний
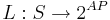$L:S \rightarrow 2^{AP}$ - функция разметки

S, Act - конечные или счётные множества

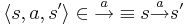
$\langle s, a, s' \rangle \in \overset{a}{\rightarrow} \equiv s \overset{a}{\rightarrow} s'$

Пример LTS: Лекция 2, слайды 40-41

Прямые потомки

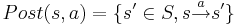$Post(s, a) = \{s' \in S, s \overset{a}{\rightarrow} s'\}$ - такие состояния s', которые непосредственно вытекают из s через переход a
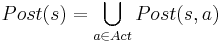$Post(s) = \bigcup_{a \in Act} Post(s, a)$ - все возможные состояния s', которые непосредственно вытекают из s

Система 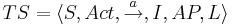$TS = \langle S, Act, \overset{a}{\rightarrow} ,I, AP, L \rangle$ детерминирована:

по действиям тогда и только тогда, когда
- $|I| \leqslant 1$
- $\forall s \in S, \forall a \in Act \Rightarrow |Post(s, a)| \leqslant 1$
по атомарным высказываниям
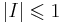
- $|I| \leqslant 1$
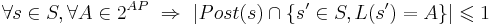- $\forall s \in S, \forall A \in 2^{AP} ~ \Rightarrow ~ |Post(s) \cap \{s' \in S, L(s') = A\}| \leqslant 1$ ( количество одинаково размеченных потомков не больше одного )

Недетерминизм - это фича! Полезен для:

моделирования параллельного выполнения в режиме чередования (интерливинга)
- позволяет не указывать скорость выполнения процессов
моделирования прототипа системы
- не ограничивает реализацию заданным порядком выполнения операторов
построения абстракции реальной системы
- модель может быть построена по неполной информации

Вычисления

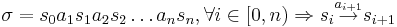
Конечный фрагмент вычисления $σ$ системы переходов TS - это конечная последовательность чередующихся состояний и действий, заканчивающаяся состоянием: $\sigma = s_0 a_1 s_1 a_2 s_2 \dots a_n s_n, \forall i \in [0,n) \Rightarrow s_i \overset{a_{i+1}}{\rightarrow} s_{i+1}$
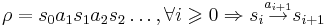
Бесконечный (максимальный) фрагмент вычисления $ρ$ - $\rho = s_0 a_1 s_1 a_2 s_2 \dots, \forall i \geqslant 0 \Rightarrow s_i \overset{a_{i+1}}{\rightarrow} s_{i+1}$
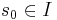
Начальный фрагмент вычисления - фрагмент вычисления, для которого $s_0 \in I$
Вычисление - начальный максимальный фрагмент вычисления

Достижимое состояние (из начального) в системе переходов TS - такое состояние 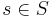$s \in S$ , для которого существует конечный фрагмент вычисления $s_0 a_1 s_1 a_2 s_2 \dots a_n s_n = s$

Reach(TS) - множество всех достижимых состояний в TS

Трасса 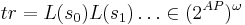$tr = L(s_0) L(s_1) \dots \in (2^{AP})^\omega$

Свойства линейного времени

Свойство 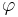$\varphi$ определяет набор допустимых трасс: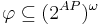 $\varphi \subseteq (2^{AP})^\omega$
Система переходов TS удовлетворяет свойству линейного времени
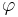
- $TS \models \varphi ~~ \Leftrightarrow ~~ Traces(TS) \subseteq \varphi$
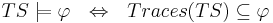
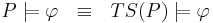- $P \models \varphi ~~ \equiv ~~ TS(P) \models \varphi$ - по определению программа удовлетворяет свойству φ, если её система переходов удовлетворяет этому свойству

Моделирование программ. Графы программ. Статическая и операционная семантика.

Граф программы – формальное описание текста программы.

$D p$ -- единый абстрактный домен данных.
P -- программа.
- $V p$ -- множество переменных программы(Var).
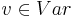
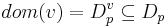- $dom(v) = D_p^v \subseteq D_p$ -- каждая переменная принадлежит какому-либо домену
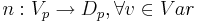
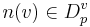
$n$ -- подстановка. $n: V_p \rightarrow D_p, \forall v \in Var$ $n(v) \in D_p^v$
Cond(V_p) -- Набор булевых условий над V_p
- формулы пропозициональной логики
- условия на переменные
$E v a l (V a r)$ -- множество значений переменных.
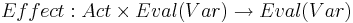
Эффект операторов: $Effect: Act \times Eval(Var) \rightarrow Eval(Var)$

Граф программы:

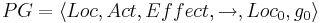
$PG= \langle Loc , Act , Effect ,\rightarrow, Loc_0, g_0 \rangle$

Loc -- множество точек
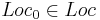- $Loc_0 \in Loc$ -- множество начальных точек
$A c t$ -- множество действий
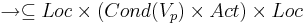$\rightarrow \subseteq Loc \times (Cond(V_p) \times Act) \times Loc$ -- отношение перехода ( $C o n d (V p)$ -- это фактически страж оператора )
$E f f e c t$ -- функция эффекта
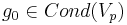$g_0 \in Cond(V_p)$ -- начальное условие

Получение TS из PG: раскрутка графа

Состояние в TS -- это точка программы и текущая подстановка
Начальное состояние -- исходная точка, удовлетворяющая начальному условию
Атомарные высказывания в TS:
- находимся в точке программы l
- значение переменной x принадлежит некоторому множеству и это множество является подмножеством множеств значений этой переменной.
Состояния 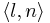$\langle l,n \rangle$ размечаются высказыванием о том, что мы находимся в точке программы l и всеми высказываниями, истинными в n
Если в графе программы есть дуга из l в $l'$ со стражем g и действием a и в некоторой подстановке n выполняется страж g, то в системе переходов, которая соответствует этой программе будет присутствовать дуга из состояния 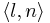$\langle l,n\rangle$ в состояние 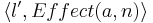$\langle l', Effect(a,n)\rangle$ по действию a.

Системы переходов графов программ Операционная семантика -- строгое описание того как из графа программы получить ее систему переходов. Описывается это все при помощи правил вывода. TS(PG) -- система переходов графа программы 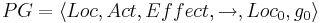$PG= \langle Loc , Act , Effect ,\rightarrow, Loc_0, g_0 \rangle$ задается сигнатурой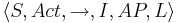 $\langle S, Act, \rightarrow, I, AP, L \rangle$

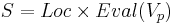$S = Loc \times Eval(V_p)$ (декартово произведение точек программы на всевозможные подстановки)
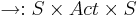$\rightarrow : S \times Act \times S$ с соответствующим правилом вывода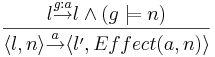 $\frac{l \overset{g:a}{\rightarrow} l \and (g \models n) }{\langle l,n \rangle \overset{a}{\rightarrow} \langle l',Effect(a,n) \rangle }$

Множество начальных состояний системы переходов описывается как множество состояний, в которых точка программы принадлежит начальным точкам, а на подстановках выполняется начальное условие графа программы:
- $I={\langle l , n \rangle : l \in Loc_0 , n \models g_0 }$
Множество атомарных высказываний -- это объединение множества точек программы и всевозможных булевых высказываний над переменными программы:
- $AP=Loc \cup Cond(V_P)$
Состояния вида 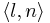размечаются высказываниям о точке программы, в которой мы находимся и всеми высказываниями из множества всевозможных высказываний, которые верны в этой подстановке:
- $L(\langle l , n \rangle)= (l) \cup (g \in Cond(V_P): n \models g ).$

Пример: Лекция 4, слайд 16

Параллелизм. Чередование систем переходов.

Лекция 4, слайды 21-24

Действия независимых процессов чередуются.
Порядок выполнения процессов не известен.

Чередование:

эффект от параллельного выполнения независимых действий a и b равен эффекту от их последовательного выполнения в произвольном порядке:
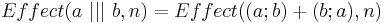
- - ||| -- оператор чередования
  - ; -- оператор последовательного выполнения
  - + -- оператор недетерминированного выбора

Пример -- слайд 23

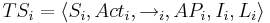
Чередование систем переходов $TS_i = \langle S_i, Act_i, \rightarrow_i, AP_i, I_i, L_i \rangle$

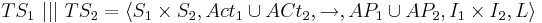
$TS_1 ~|||~ TS_2= \langle S_1 \times S_2, Act_1 \cup ACt_2, \rightarrow, AP_1 \cup AP_2, I_1 \times I_2, L \rangle$

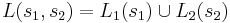
$L(s_1, s_2)= L_1(s_1) \cup L_2(s_2)$

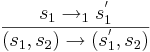
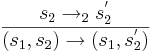
$\frac{s_1 \rightarrow_1 s_1^'}{(s_1, s_2) \rightarrow (s_1^', s_2)}$ $\frac{s_2 \rightarrow_2 s_2^'}{(s_1, s_2) \rightarrow (s_1, s_2^')}$

Параллелизм. Чередование графов программ. Случаи без разделяемых переменных и с разделяемыми переменными.

Параллелизм. Синхронный параллелизм. Рандеву.

распределённые программы выполняются параллельно
в распределённой программе нет разделяемых переменных

Передача сообщений в распределённых программах:

cинхронная передача сообщений (рандеву)
асинхронная передача сообщений (кналы)

Синхронный обмен сообщенийями:

Процессы вместе выполняют синхронизированные действия
Взаимодействие процессов - одновременно

Рандеву

$TS_i = \langle S_i, Act_i, \overset{a}{\rightarrow}_i ,I_i, AP_i, L_i \rangle ~~~ i=\{1,2\}$
$H \subseteq Act_1 \cap Act_2$

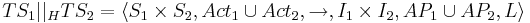Тогда $TS_1 ||_H TS_2= \langle S_1 \times S_2, Act_1 \cup Act_2, \rightarrow, I_1 \times I_2, AP_1 \cup AP_2, L \rangle$ , где

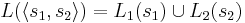
$L(\langle s_1, s_2 \rangle) = L_1(s_1) \cup L_2(s_2)$
определяется как:
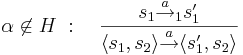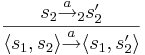
- интерливинг для $\alpha \not\in H~:~~~ \frac{s_1 \overset{a}{\rightarrow}_1 s_1'}{ \langle s_1, s_2 \rangle \overset{a}{\rightarrow} \langle s_1', s_2 \rangle}$ и $\frac{s_2 \overset{a}{\rightarrow}_2 s_2'}{ \langle s_1, s_2 \rangle \overset{a}{\rightarrow} \langle s_1, s_2' \rangle}$
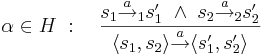
- рандеву для $\alpha \in H~:~~~ \frac{s_1 \overset{a}{\rightarrow}_1 s_1' ~ \wedge ~ s_2 \overset{a}{\rightarrow}_2 s_2'}{ \langle s_1, s_2 \rangle \overset{a}{\rightarrow} \langle s_1', s_2' \rangle}$

Пример рандеву: Лекция 4, слайд 32

Синхронный параллелизм

$TS_i = \langle S_i, Act_i, \overset{a}{\rightarrow}_i ,I_i, AP_i, L_i \rangle ~~~ i=\{1,2\}$
$Act_1 \times Act_2 \rightarrow Act ~~ : ~~ (\alpha, \beta) \rightarrow \alpha * \beta$

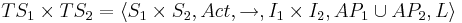Тогда $TS_1 \times TS_2 = \langle S_1 \times S_2, Act, \rightarrow, I_1 \times I_2, AP_1 \cup AP_2, L \rangle$ , где

$L(\langle s_1, s_2 \rangle) = L_1(s_1) \cup L_2(s_2)$
$\rightarrow$ определяется как: $\frac{s_1 \overset{\alpha}{\rightarrow}_1 s_1' ~ \wedge ~ s_2 \overset{\beta}{\rightarrow}_2 s_2'}{ \langle s_1, s_2 \rangle \overset{\alpha * \beta}{\rightarrow} \langle s_1', s_2 \rangle}$

Параллелизм. Асинхронный параллелизм. Системы с каналами. Операционная семантика.

Абстракция. Абстракция трасс. Абстракция системы переходов. Необходимое и достаточное условие корректности LTS модели.

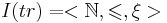
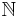Представим трассу в форме интерпретации I: $I(tr) = <\mathbb{N}, \leqslant, \xi>$

$\mathbb{N}$ - множество натуральных чисел
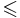$\leqslant$ - отношение порядка на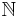 $\mathbb{N}$
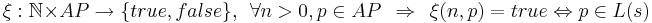$\xi: \mathbb{N} \times AP \rightarrow \{true, false\}, ~~ \forall n>0, p \in AP ~~ \Rightarrow ~~ \xi(n, p) = true \Leftrightarrow p \in L(s)$ (для каждого порядкового номера говорит истенен или ложен заданный на нем предикат)

Рассмотрим трассы tr и tr' такие, что

$I(tr) = <\mathbb{N}, \leqslant, \xi>, ~~ \xi: \mathbb{N} \times AP = \{true, false\}$
$I(tr) = <\mathbb{N}, \leqslant, \xi'>, ~~ \xi: \mathbb{N} \times AP' = \{true, false\}$

Будем говорить, что трасса tr' является абстракцией трассы tr (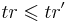 $tr \leqslant tr'$ ), если

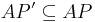
$AP' \subseteq AP$
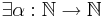$\exists \alpha : \mathbb{N} \rightarrow \mathbb{N}$ такое, что 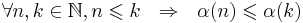$\forall n,k \in \mathbb{N}, n \leqslant k ~~ \Rightarrow ~~ \alpha(n) \leqslant \alpha(k)$ - некоторая неубывающая функция [?]
$\forall n \in \mathbb{N}, p \in AP' ~~ \Rightarrow ~~ \xi(n, p) = \xi'(\alpha(n), p)$

Пример абстракции трассы: Лекция 2, слайд 53

Необходимое условие корректности модели - 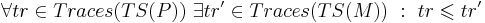$\forall tr \in Traces(TS(P)) ~ \exists tr' \in Traces(TS(M)) ~ : ~ tr \leqslant tr'$ , где

$P$ - система
$M$ - модель этой системы

При этом, если 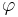$\varphi$ - некоторое свойство системы, то 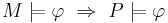$M \models \varphi ~ \Rightarrow ~ P \models \varphi$ выполняется тогда и только тогда, когда верно условие корректности модели.

Абстракция. Абстракция системы переходов. Достаточное условие корректности LTS модели. Адекватность LTS модели.

Абстракция системы переходов -- картинка на 4 слайде 3-й лекции.

Достаточное условие корректности LTS модели.

Пусть у нас имеются две системы переходов, $T S 1$ и $T S 2$ -- для системы и модели соответственно:

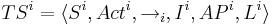
$TS^i = \langle S^i, Act^i, \rightarrow_i, I^i, AP^i, L^i \rangle$

Достаточное условие корректности:

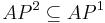
Алфавит предикатов модели включен в алафвит предикатов системы: $AP^2 \sube AP^1$
Задано отображение 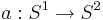. На отображение накладываются следующие условия:
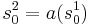
- Оно преобразует начальное состояние системы в начальное состояние модели: $s^2_0 = a(s^1_0)$
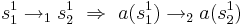
- Каждому переходу из системы должен соответствовать переход в модели: $s^1_1 \rightarrow_1 s^1_2 ~ \Rightarrow ~ a(s^1_1) \rightarrow_2 a(s^1_2)$
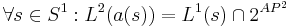
Метки на состояниях модели должны состоять только из предикатов модели: $\forall s \in S^1: L^2(a(s)) = L^1(s) \cap 2^{AP^2}$

Необходимое (но не достаточное) [?] условие адекватности модели свойствам правильности :

Алфавит предикатов свойств правильности включен в алфавит предикатов модели.

Абстракция. Абстракция графов программ. Отношение слабой симуляции.

Лекция 10, слайды 8 - 11

Программа PG' корректно моделирует программу PG тогда и только тогда, когда система переходов TS(PG') корректно моделирует систему переходов TS(PG).

Будем говорить, что PG' моделирует PG, если

в PG' присутствуют переменные, соответствующие наблюдаемым переменным PG
все действия PG, влияющие на наблюдаемые переменные, отражены в модели (наблюдаемые операторы)
модель корректно воспроизводит возможные последовательности изменения значений наблюдаемых переменных, присутствующих в PG

Отношение слабой симуляции не сохраняет количество шагов между состояниями. В связи с этим, не сохраняются свойства, не инвариантные к прореживанию (LTL: оператор neXt).

Логика LTL, автоматы Бюхи

Свойства правильности. Формулирование требований правильности программы. Двойственность. Типы свойств.

Требования правильности -- утверждения о возможных и невозможных вариантах выполнения программы.

Двойственность :

если какое-то утверждение невозможно, то обратное -- неизбежно
если какое-то утверждение неизбежно, то обратное -- невозможно
при помощи логики от одного можно переходить к другому при помощи отрицания

Способы описания свойств правильности:

свойства достижимых состояний (свойства безопасности)
свойства последовательности состояний (свойства живучести)
в Promela:
- свойства состояний
  - asserts
    - локальные ассерты процессов
    - инварианты системы процессов
  - метки терминальных состояний
    - задаём допустимые точки останова прочесса
- свойства последовательностей состояний
  - метки прогресса - чтобы найти циклы бездействия
  - утверждения о невозможности (never claims) - например, LTL формулы
  - трассовые ассерты - используются для описания правильных последовательностей выполнения операторов отправки и приема сообщения

Свойства правильности. Свойства безопасности и живучести. Проверка таких свойств. Примеры свойств.

Типы свойств:

свойства безопасности
- ничего плохого никогда не произойдет
- пример: инвариант системы (например, x всегда меньше y);
- задача верификатора -- найти те вычисления, которые ведут к нарушению безопасности.
свойства живучести
- рано или поздно произойдет что-то хорошее
- пример: “отзывчивость” (например, если отправлен запрос, то рано или поздно будет сгенерирован ответ)
- задача верификатора – найти вычисления, в которых это “хорошее” может откладываться до бесконечности.

Автоматы Бюхи. Конечные автоматы. Проход автомата. Язык автомата.

Лекция 6, слайды 8 - 15

Конечный автомат описывается сигнатурой: 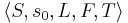$\langle S, s_0, L, F, T\rangle$ , где

S -- множество сотояний
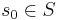$s_0 \in S$ -- множество начальных состояний
L -- конечное множество меток
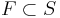$F \subset S$ -- множество терминальных состояний
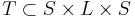$T \subset S \times L \times S$ -- отношение перехода на состояниях

Детерминизм и недетерминизм

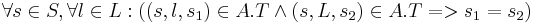
Конечный автомат называется детерминированным, если по метке и исходному состоянию можно однозначно определить целевое состояние: $\forall s \in S, \forall l \in L: ((s, l, s_1) \in A.T \and (s, L, s_2) \in A.T => s_1 = s_2)$

В противном случае автомат называется недетерминированным.

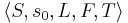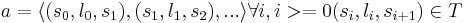
Проходом a конечного автомата $\langle S,s_0,L,F,T \rangle$ называется такое упорядоченное и, возможно, бесконечное множеств переходов из T: $a=\langle (s_0, l_0, s_1),(s_1, l_1, s_2), ... \rangle \forall i, i >= 0 (s_i, l_{i}, s_{i+1}) \in T$

Допускающим проходом конечного автомата A называется конечный проход a, финальный переход которого ( $s n - 1, l n - 1, s n)$ ведёт в терминальное состояние.

Языком автомата A называется множество слов в алфавите A.L, соответствующих допускающим проходам автомата А

Автоматы Бюхи. Омега-допускание. Расширение автоматов Бюхи.

Лекция 6, слайды 16

Допускающий проход по Бюхи(w-допускание) конечного автомата A называется такой бесконечный проход a, что 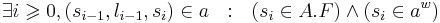$\exists i \geqslant 0, (s_{i-1}, l_{i-1}, s_i) \in a ~~ : ~~ (s_{i} \in A.F) \and (s_{i} \in a^w)$

т.е. по крайней мере одно терминальное состояние встречается бесконечно часто.

Расширение автоматов Бюхи.

Конечные проходы дополняются бесконечным переходом по пустому действию. При помощи автоматов Бюхи удобно проверять свойства живучести.

Логика LTL. Синтаксис LTL. Семантика выполнимости формул. Сильный и слабый until.

Лекция 6, слайды 30 - 35

Особенности LTL:

может использоваться для описания свойств как живучести, так и безопасности
описывает свойства, которым должны удовлетворять линейные последовательности наблюдаемых состояний - трассы
семантика LTL определена на бесконечных автоматах Бюхи. Для конечных проходов необходимо использовать расширение автоматаю

Формула в LTL f::=

p, q, ... -- свойства состояний, включая true и false
(f) -- группировка при помощи скобок
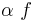$\alpha ~ f$ -- унарные операторы
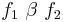$f_1 ~ \beta ~ f_2$ -- бинарные операторы

Операторы в LTL

унарные
- $\Box$ ([]) -- всегда в будущем
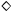- $\diamond$ (<>) -- в конце концов
- $X$ (X) -- в следующем состоянии
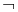- $\neg$ (!) -- логическое отрицание
бинарные
- $U$ (U) -- до тех пор, пока
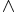- $\wedge$ (&&) -- логическое И
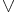- $\vee$ (||) -- логическое ИЛИ
- $\rightarrow$ (->) -- логическая импликация
- $\leftrightarrow$ (<->) -- логическая эквивалентность

Сильный Until:

всегда e, до тех пор, пока не f, при этом f обязательно должно наступить
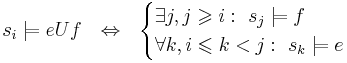
$s_i \models e U f ~~ \Leftrightarrow ~~ \begin{cases} \exists j, j \geqslant i: ~ s_j \models f \\ \forall k, i \leqslant k < j: ~ s_k \models e \end{cases}$

Слабый Until:

всегда e, до тех пор, пока не f, при этом не факт, что f наступает (тогда всегда e)
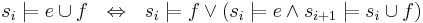
$s_i \models e \cup f ~~ \Leftrightarrow ~~ s_i \models f \vee (s_i \models e \wedge s_{i+1} \models s_i \cup f)$

Выполнимость формул:

Задаётся последовательность состояний прохода $σ$
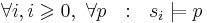$\forall i, i \geqslant 0, ~ \forall p ~~ : ~~ s_i \models p$ Внимание!! это слишком смахивает на бред, который должен быть интуитивно понятен. Если кто может - распишите подробнее выполнимость!!

Логика LTL. Основные типы свойств LTL. Цикличность, стабильность, инвариант, гарантия, отклик, приоритет, корреляция.

Лекция 6, Слайды 38-39

Распространенные LTL-формулы
Формула	Описание	Тип
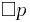$\Box p$	всегда p	инвариант
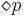$\diamond p$	рано или поздно p	гарантия
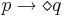$p \rightarrow \diamond q$	если p, то рано или поздно q	отклик
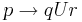$p \rightarrow q U r$	если p то затем q и рано или поздно r	приоритет
$\Box\diamond p$	всегда рано или позндно будет p	цикличность (прогресс)
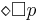$\diamond\Box p$	рано или позндно всегда будет p	стабильность (бездействие)
$\diamond p \rightarrow \diamond q$	если рано или поздно p, то рано или поздно q	корреляция

Логика LTL. Эквивалентные преобразования формул LTL.

Лекция 6, Слайды 40

$\begin{align} \neg\Box p & \Leftrightarrow & \diamond \neg p \\ \neg\diamond p & \Leftrightarrow & \Box \neg p \\ & & \\ \neg(p U q) & \Leftrightarrow & \neg q \cup (\neg p \wedge \neg q) \\ \neg(p \cup q) & \Leftrightarrow & \neg q U (\neg p \wedge \neg q) \\ & & \\ \Box (p \wedge q) & \Leftrightarrow & \Box p \wedge \Box q \\ \diamond (p \vee q) & \Leftrightarrow & \diamond p \vee \diamond q \\ \end{align}$

$\begin{align} p \cup (q \vee r) & \Leftrightarrow & (p \cup q) \vee (p \cup r) \\ (p \wedge q) \cup r & \Leftrightarrow & (p \cup r) \wedge (q \cup r) \\ & & \\ p U (q \vee r) & \Leftrightarrow & (p U q) \vee (p U r) \\ (p U q) \cup r & \Leftrightarrow & (p U r) \wedge (q U r) \\ & & \\ \Box\diamond (p \wedge q) & \Leftrightarrow & \Box\diamond p \wedge \Box\diamond q \\ \diamond\Box (p \vee q) & \Leftrightarrow & \diamond\Box p \vee \diamond\Box q \\ \end{align}$

Логика LTL. Оператор neXt. Свойства, инвариантные к прореживанию.

Оператор X нужно использовать аккуратно:

с его помощью делается утверждение о выполнимости формулы на непосредственных потомках текущего состояния,
в распределённых системах значение оператора X неочевидно,
поскольку алгоритм планирования процессов неизвестен, не стоит формулировать спецификацию в предположении о том,

какое состояние будет следующим,

стоит ограничиться предположением о справедливости планирования.

Свойства, инвариантные к прореживанию

Пусть f – трасса некоторого вычисления над пропозициональными формулами P,
- по трассе можно определить, выполняется ли на ней темпоральная формула,
- трассу можно записать в форме:
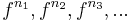  - $f^{n_1}, f^{n_2},f^{n_3}, ...$ -- где значения пропозициональных формул на каждом интервале совпадают.
Обозначим E(f) набор всех трасс, отличающихся лишь значениями n₁,n₂,n₃ (т.е. длиной интервалов).
- E(f) называется расширением прореживания f.

Свойство ψ, инвариантное к прореживанию, либо истинно для всех трасс из E(ψ), либо ни для одной из них:
- $\psi \models f => \forall v \in E(\psi), v \models f$
истинность такого свойства не зависит от длины трассы, а только от порядка, в котором пропозициональные формулы

меняют свои значения;

Теорема: все формулы LTL без оператора X инвариантны к

прореживанию.

Логика LTL. Проверка выполнимости формул LTL при помощи автоматов Бюхи. Проверка LTL-формул в Spin.

Связь LTL с автоматами Бюхи

Удобно проверять допустимость трасс для некоторого автомата Бюхи;
Удобно описывать свойства правильности при помощи темпоральных формул;
Для всякой LTL-формулы f существует автомат Бюхи, который допускает те и только те прогоны, которым соответствуют трассы, на которых выполнима f;

Переход от LTL к автоматам

Привести свойство правильности LTL к форме never языка Promela достаточно просто: нужно построить отрицание LTL формулы и поместить его в тело never:
- f выполняется на всех вычислениях <=>
- !f не выполняется ни на одном вычислении <=>
- автомат never {!f} не допускает ни одного прогона, полученного в результате синхронного выполнения с системой

Логика LTL. Выразительная мощность LTL. Логики LTL + существование, CTL* и CTL. Сравнение выразительной мощности.

При помощи конструкции never можно описать любой w-регулярный автомат над словами Выразительная мощность LTL

по сравнению с конструкциями never

LTL описывает подмножество этого языка:
- всё, выразимое на LTL, может быть описано при помощи never,
- при помощи never можно описать свойства, не выразимые на LTL
Добавление одного квантора существования над одним пропозициональным символом расширяет выразительные способности LTL до всех омега-регулярных автоматов над словами.

(p) может быть истинным после выполнения системой чётного количества шагов, но никогда не истинно после нечётного.

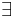$\exists$ t.t && [](t -> X!t) && [](!t -> Xt) && [](!t -> !p)

LTL-формула описывает свойство, которое должно выполняться на всех вычислениях, начинающихся из исходного остояния системы

Логика СTL*

Логика ветвящегося времени:
- использует кванторы ∀ и ∃
- использует F вместо <> и G вместо []

Логика СTL

Логика CTL – фрагмент логики CTL*, в котором под управлением квантора пути (E или A) может находиться не более дного оператора X или U

Выразительные возможности CTL* и CTL

CTL* и CTL описывают подмножества w-регулярных автоматов над деревьями
- автоматы над деревьями более выразительны, чем автоматы над словами (CTL-формула выполнима на дереве трасс, а не на одной трассе);
CTL и LTL являются подмножествами CTL*;
CTL и LTL не сравнимы по выразительной мощности (пересекаются, но не включают);
на LTL можно описать свойства, не выразимые на CTL:
- CTL не позволяет описать свойства вида []<>(p),
- при помощи []<>(p) в LTL задаются ограничения справедливости;
на CTL можно описать свойства, не выразимые на LTL:
- на LTL нельзя описать свойства вида AGEF(p),
- AGEF(p) используется для описания свойства reset: из любого состояния

система может перейти в нормальное

Верификация программ на моделях

Задача проверки правильности программ. Валидация. Верификация. Системы с повышенными требованиями к надёжности. Реактивные программы. Параллельные программы. Особенности верификации таких программ.

Валидация - исследование и обоснование того, что спецификация ПО и само ПО через реализованную в нём функциональность удовлетворяет ребованиям пользователей.

Верификация - исследование и обоснование того, что программа соответствует своей спецификации.

Верификация в общем случае алгоритмически неразрешима.

Методы верификации:

"Полное" тестирование (слайды 14-22)
Имитационное моделирование
Доказательство теорем (27-29)
Статический анализ (30-33)
Верификация на моделях (34-38)

Типы программ:

Традиционные программы
- завершимость
- спецификация включает в себя описание входа/выхода программы
- число состояний зависит от входных данных и переменных
Реактивные программы
- работают в бесконечном цикле
- взаимодействуют с окружением
- спецификация представляет собой пары стимул/реакция
Параллельные программы
- совместная работа нескольких компонент
- невоспроизводимость тестов
- ограниченные возможности по наблюдению

Подходы к верификации программ. Тестирование и имитационное моделирование. Область применения, плюсы и минусы. Проблема полноты тестового покрытия.

Подходы к верификации программ. Доказательство теорем. Область применения, плюсы и минусы.

Основные пункты:

система и её свойста - формулы
задан набор аксиом и правил вывода
строится доказательство свойства-теоремы
таким образом, производится качественный анализ системы

Пример: Лекция 1, слайд 28

Достоинства:

работа с бесконечными пространствами состояний
даёт более глубокое понимание системы

Недостатки

медленная скорость работы
может потребоваться помощь человека (построение инвариантов циклов)
в общем случае нельзя построить полную систему аксиом и правил вывода

Подходы к верификации программ. Статический анализ исходного кода программ. Область применения, плюсы и минусы.

Статистический анализ -- оцениваем для каждого состояния программы потенциально возможные значения переменных.

Пример: Лекция 1, Слайды 31-32

Особенности:

анализ исходного текста без запуска программы
в общем случае задача неразрешима

Достоинства:

высокая скорость работы
если ответ дан - ему можно верить

Недостатки:

узкая область применения: компиляторы, анализ похожести кода, анализ безопасности
ручная настройка при изменении применяемых свойств

Подходы к верификации программ. Верификация программ на моделях. Процесс верификации программы при помощи её модели. Область применения, плюсы и минусы.

Лекция 1, Слайды 34-38 , 45

Особенности:

проверка свойств на конечной модели
исчерпывающий поиск по пространству состояний
свойства задаются в терминах значений предикатов состояний программы или последовательности этих значений

Пример: Лекция 1, слайды 35-36

Процесс верификации программ на моделях:

моделирование
- построение адекватной, корректной модели
- фильтрация "лишних" состояний
спецификация свойств
- темпоральная логика
- полнота свойств
верификация
- построение контр-примера
- анализ контр-примера

Достоинтсва:

хорошая автоматизация
если модель конечна, корректна и адекватна данному свойству, то будет получен точный ответ
выявление редких ошибок

Недостатки:

работает только для конечных моделей

Области применения

сетевые и криптографические протоколы
протоколы работы кэш-памяти
интегральные схемы
стандарты
встроенные системы
драйвера
и прочие программы на C

Верификация на моделях. История развития верификации программ на моделях. Схема верификации программ на моделях. Классы проверяемых свойств правильности программы.

Лекция 1, Слайды 40-44

Лекция 2, Слайды 3-4

Примеры классов свойств:

Стандартные
- deadlocks (взаимная блокировка)
- Race condition (состояние гонки)
Специфичные для конкретного приложения
- требования справедливости
- корректная завершаемость
- причинно-следственный и темпоральный порядок состояний системы

Схема верификации на модели: Лекция 2, слайд 3

Верификация при помощи Spin. Задание свойств состояний.

Cвойства состояний

asserts
- локальные ассерты процессов
- инварианты системы процессов
  - active proctype invariant() { assert(something)}
метки терминальных состояний
- задаём допустимые точки останова процесса
  - метка end -- система не может завершить работу без того, чтобы все активные процессы либо завершились, либо остановились в точках, помеченных метками end;

Верификация при помощи Spin. Задание свойств последовательностей состояний. Циклы бездействия. Ограничения справедливости.

Свойства последовательностей состояний

метки прогресса (чтобы найти циклы бездействия)
утверждения о невозможности (never claims)
- например, определяются LTL-формулами
трассовые ассерты

Циклы бездействия. Мы хотим найти потенциально бесконечные циклы, не выполняющие никакой полезной работы. Помечаем меткой progress полезные операторы. Если найдется цикл, работающий потенциально бесконечно и не проходящий по метке progress, верификатор выдаст ошибку.

Ограничения справедливости. Существует два основных варианта справедливости:

слабая справедливость:
- если оператор выполним бесконечно долго, то он в конце концов будет выполнен
сильная справедливость:
- если оператор выполним бесконечно часто,то он в конце концов будет выполнен.

Справедливость применима как к внутреннему, так и к внешнему недетерминизму. Использование сильной справедливости – существенно дороже слабой

Верификация при помощи Spin. Задание свойств последовательностей состояний. Утверждения о невозможности. Трассовые ассерты.

never claims (утверждения о невозможности):

выполняются синхронно с моделью,
если достигнут конец, то – ошибка,
состоят из выражений и конструкция задания

потока управления

фактически, описывают распознающий

автомат.

Конструкция never

может быть как детерминированной, так и нет;
содержит только выражения без побочных эффектов (соотв. булевым высказываниям на состояниях);
используются для описания неправильного поведения системы;
прерывается при блокировании:
- блокируется => наблюдаемое поведение не соответствует описанному,
- паузы в выполнении тела never должны быть явно заданы как бесконечные циклы;
never нарушается, если:
- достигнута закрывающая скобка,
- завершена конструкция accept (допускающий цикл);
бездействие может быть описано как конструкция never или её часть (для цикла бездействия есть тело never по умолчанию).

Видимость

все конструкции never – глобальны;
тем самым, в них можно ссылаться на
- глобальные переменные,
- каналы сообщений,
- точки описания процессов (метки),
- предопределённые глобальные переменные,
- но не локальные переменные процессов;

Ассерты на трассы Используются для описания выполнения прывильных и неправильных последовательностей операторов send и recieve

Верификация при помощи Spin. Принцип верификации нарушения свойств. Контрпримеры. Процесс верификации при помощи Spin. Использование LTL в Spin.

Система Spin и язык Promela

Система Spin. Процесс моделирования и верификации при помощи системы Spin. Конечность моделей на Promela. Асинхронное выполнение моделей. Недетерминированный поток управления. Понятие выполнимости оператора.

Язык Promela. Основные компоненты модели на языке Promela. Процессы, локальные и глобальные объекты данных, каналы сообщений.

Язык Promela. Механизмы взаимодействия процессов в языке Promela. Глобальные переменные, каналы сообщений, явная синхронизация.

Язык Promela. Основные операторы языка Promela. Операторы-выражения, присваивания.

Язык Promela. Основные операторы языка Promela. Отладочная печать, операторы skip, true, run, assert.

Язык Promela. Чередование (интерливинг) операторов. Внешний и внутренний недетерминизм. Управление выполнимостью операторов.

Язык Promela. Задание потока управления последовательного процесса. Управляющие конструкции if, do. Организация внутреннего недетерминизма.

Язык Promela. Каналы сообщений. Операторы отправки и приёма сообщений. Тип mtype. синхронная и асинхронная передача сообщений.

Язык Promela. Каналы сообщений. Вспомогательные операции с каналами сообщений.

Язык Promela. Основные типы данных. Область видимости данных.

Получено с http://esyr.us/wiki/%D0%92%D0%9F%D0%BD%D0%9C/%D0%A2%D0%B5%D0%BE%D1%80%D0%BC%D0%B8%D0%BD

@@ Строка 138: / Строка 138: @@
 '''Чередование:'''
 * эффект от параллельного выполнения независимых действий a и b равен эффекту от их последовательного выполнения в произвольном порядке:
-** <math>Effect(a lll b,n) = Effect((a;b)+(b;a),n)</math>
+** <math>Effect(a ~|||~ b,n) = Effect((a;b)+(b;a),n)</math>
-*** lll -- оператор чередования
+*** ||| -- оператор чередования
 *** ; -- оператор последовательного выполнения
 *** + -- оператор недетерминированного выбора
@@ Строка 147: / Строка 147: @@
 <math>TS_i = \langle S_i, Act_i, \rightarrow_i, AP_i, I_i, L_i \rangle</math>
-<math>TS_1 lll TS_2= \langle S_1 \times S_2, Act_1 \cup ACt_2, \rightarrow, AP_1 \cup AP_2, I_1 \times I_2, L \rangle</math>
+<math>TS_1 ~|||~ TS_2= \langle S_1 \times S_2, Act_1 \cup ACt_2, \rightarrow, AP_1 \cup AP_2, I_1 \times I_2, L \rangle</math>
 <math>L(s_1, s_2)= L_1(s_1) \cup L_2(s_2) </math>