Основы Кибернетики, Алгоритмы решения задач/Задачи на синтез схем
Материал из eSyr's wiki.
По заданной ФАЛ с помощью простейших методов, метода каскадов или метода Шеннона построить реализующую ее СФЭ или КС.
Простейшие методы
Промежуточные действия
- Если ФАЛ представлена в виде таблицы, то построим по ней сокращённую ДНФ (как объединение всех возможных случаев, когда она равна 1).
- Если ФАЛ представлена в виде формулы, преобразуем ее, чтобы остались только функции базиса Б0. Кроме того, поднимаем все отрицания (они должны стоять над только переменными, но не над бо́льшими кусками выражения).
Получение СФЭ
Строим как-нибудь подвыражения в соответствии с приоритетом операций. Поскольку оставлены только функции базиса Б0, то это не вызывает особых затруднений. Что вижу, то и рисую.
Получение КС
Разбираем формулу
- A ∨ B преобразуем в ветвление, где один вариант реализует A, а другой — B
- A & B преобразуем в последовательное соединение, где первая часть реализует A, другая — B.
- xi преобразуем в контакт с меткой xi
- xi преобразуем в контакт с меткой xi
Метод каскадов
Промежуточные действия
Пусть у нас имеются булевы функции F1(x1,x2,...xn),...,Fk(x1,x2,...xn), зависящие от n переменных. Обозначим следующее множество:
M0 = {F1(x1,x2,...xn),...,Fk(x1,x2,...xn)}.
В простейшем случае, в нем одна функция. Воспользуемся следующим приемом:
F(x1,x2,...xn)=x1*F(1,x2,...xn)V x1*F(0,x2,...xn)
Тогда определим правило построения следующих множеств (M1,M2,...,Mn):
Mi+1 = {g(0,xi+1,...xn)|g∈Mi} U {g(1,xi+1,...xn)|g∈Mi}.
Если функция представлена строкой значений, то формируем новое множество из левых и правых половин. Если функция представлена формулой, то подставляем в нее xi=0 и xi=1 и упрощаем. При этом после построения из Mi удаляются все фунции, несущественно зависящие от x1 (для строк значений это хорошо видно, т.к. левая и правая половина совпадает)
Пример
f1(x1,x2,x3,x4)=(1000 0010 1111 1000) f2(x1,x2,x3,x4)=(1000 1111 0010 1000)
- M0={(1000 0010 1111 1000),(1000 1111 0010 1000)}
- M1={(1000 0010),(1111 1000),(1000 1111),(0010 1000)}
- M2={(1000),(0010),
(1111)} - M3={(10),
(00),(11)} - M4={0,1}
Получение СФЭ
Реализуем на базе любого входа
- 0 = xi & xi
- 1 = xi V xi
Для реализации элемента Mi используем элементы Mi+1: пусть f(0,xi+1,...xn)=g(xi+1,...xn) и f(1,xi+1,...xn)=h(xi+1,...xn).
Тогда для реализации f соединеним дизъюнкцией конъюнкцию g и xi с конъюнкцией h и xi.
Реализацию элементов M0 метим как выходы СФЭ.
Получение КС
Обозначаем все элементы всех множеств узлами КС.
- если g(xi+1,...xn)=h(0,xi+1,...xn), то соединаям g и h контактом с меткой xi
- если g(xi+1,...xn)=h(1,xi+1,...xn), то соединаям g и h контактом с меткой xi
После этого удаляем вершину с меткой 0 и все ведущие в нее контакты. Вершину с меткой 1, а также F1,...,Fk помечаем как входы КС.
Метод Шеннона
Промежуточные действия
Выбираем некоторое 1≤q≤n. Расклыдаваем исходное f(x',x") = V xi+1σi+1 & xi+2σi+2 & ... & xnσn & fσ"(x'). Обычно выбирают q = округленноый вниз(log2(n-2*log2(n))). После чего составляется универсальный многополюсник порядка q(имеющий q входов и 2n выходов) и мультиплексор порядка n-q (зависщий от адресных переменных xi+1, ... ,xn и от выходов универсального многополюсника, выдающий на выход fσ"(x') в соответствии с приведенной формулой в свой единственный выход).
Данный метод не применяется на практике для построения КС или СФЭ, это скорее мысленный эксперимент вроде падающего из окна Дэвида Дойча или квантового самоубийцы, используемый затем Шенноном и его последователями для оценки функции Шеннона...
Получение СФЭ
Универсальный многополюсник в СФЭ выглядит так: Мультиплексор порядка q для f(x) в СФЭ выгладит так:
Получение КС
Универсальный многополюсник в КС выглядит так: точно так же как в методе каскадов к каждой вершине приписываем x1 или x1, дабы соединить с новой волной вершин. В каждой следующем множестве будет в 2 раза больше вершин. Мультиплексор порядка q для f(x) в КС выгладит так:
Оценить сверху или снизу сложность конкретной ФАЛ или сложность самой сложной ФАЛ из заданного множества в заданном классе схем.
Оценка сложности самой сложной ФАЛ из класса
Для того, что посчитать сложность самой сложной ФАЛ из некоторого класса Q(n) ∈ P2(n), то есть, иначе говоря, вычислить функцию Шеннона, связанную с классом Q(n) (и для некоторого класса cхем U — например, СФЭ или КС), необходимо выполнить следующие шаги:
- Посчитать число функций в заданном классе Q(n).
- Сразу же из этого получить асимптотически нижнюю оценку функции Шеннона, связанной с классом Q(n):
- LK(Q(n)) ≳ log(|Q(n)|) / n
- LC(Q(n)) ≳ log(|Q(n)|) / n
- Показать, как для любой функции из данного класса построить схему из класса U, реализующую данную функцию и имеющую сложность, асимптотически равную вычисленной нижней оценке. Из этого будет следовать, что полученная асимптотически нижняя оценка является и асимптотически верхней оценкой, а из этого, в свою очередь, будет следовать, что функция Шеннона для заданного класса U(n) будет просто асимптотически равна полученной нижней оценке.
- В пункте 3 всегда пригождается следующее: для любой функции от n переменных можно построить, реализующую её СФЭ и КС со сложностью, асимптотически не превосходящей 2n / n
Пример
- Посчитать функцию Шеннона, связанную с классом самодвойственных функций, для класса СФЭ.
- Самодвойственная функция f: f(x1, …, xn) = f(x1, …, xn)
Решение
- Первый пункт является самым главным. В нём нужно получить некоторую формулу, в которой любая функция из заданного класса выражается через функцию от меньшего числа переменных. Полученная формула пригодится и впоследствии. Например, для класса самодвойственных функций, разложим функцию f по первой переменной f(x1, x2, …, xn) = x1 & f(0, x2, …, xn) ∨ x1 & f(1, x2, …, xn) = x1 & f(0, x2, …, xn) ∨ x1 & f(0, x2, …, xn) = x1 & f0(x2, …, xn) ∨ x1 & f0(x2, …, xn), где f0 = f(0, x2, …, xn). Перепишем это в виде f(x1, …, xn) = x1 ⊕ f0(x2 ⊕ x1, …, xn ⊕ x1) (*). Теперь видно, самодвойственная функция от n переменных однозначно определяется функцией f0 от n − 1 переменной, и, следовательно, число самодвойственных функций от n переменных равно 22n − 1. В принципе, это и ежу очевидно, но полученная нами (*) потребуется нам в дальнейшем.
- Из пункта 1 следует что LC(Q(n)) ≳ 2n − 1 / n
- Из (*), а также из утверждения строим схему для произвольной самодвойственной функции. Строим f0 (сложность 2n − 1 / (n − 1)). Для n «⊕» потребуется ещё не более, чем C × n функциональных элементов. В итоге как раз и получится, что сложность результирующей схемы асимптотически не превосходит 2n − 1 / n
Пример
- Посчитать функцию Шеннона, также для класса СФЭ, связанную с классом функций, таких, что:
f(x1, x2, x3, …, xn) = f(x3, x1, x2, …, xn)
Решение
- Разлагаем f по первым трём переменным:
- f(x1, x2, x3, x4, …, xn) = x1 & x2 & x3 & f(0, 0, 0, x4, …, xn) ∨ x1 & x2 & x3 & f(0, 0, 1, x4, …, xn) ∨ x1 & x2 & x3 & f(0, 1, 0, x4, …, xn) ∨ x1 & x2 & x3 & f(0, 1, 1, x4, …, xn) ∨ x1 & x2 & x3 & f(1, 0, 0, x4, …, xn) ∨ x1 & x2 & x3 & f(1, 0, 1, x4, …, xn) ∨ x1 & x2 & x3 & f(1, 1, 0, x4, …, xn) ∨ x1 & x2 & x3 & f(1, 1, 1, x4, …, xn) = (x1x2x3 ∨ x1x2x3) & fa ∨ ((x1x2x3 ∨ x1x2x3)) & fb (*), где fa = f(0, 0, 0, x4, …, xn) = f(1, 0, 0, x4, …, xn) = f(1, 1, 0, x4, …, xn) = f(1, 1,1,x4,...,xn) = f(0, 1, 1, x4, …, xn) = f(0, 0, 1, x4, …, xn); fb = f(0, 1, 0, x4, …, xn) = f(1, 0, 1, x4, …, xn). Теперь видно, что функция из данного класса однозначно определяется парой (fa, fb), где fa, fb — функции от n − 3 переменных. Таким образом, число функций из заданного класса равно числу таких пар, т. е. 22n − 3 × 22n − 3 = 22n − 2
- Из (1) следует, что LC(Q(n)) ≳ 2n − 2 / n
- Опять же, из (*) ясно, как строить схему для произвольной функции из заданного класса. Строим СФЭ для функций fa, fb (сложность каждой ≤ (2n − 3 / (n − 3)). И, кроме того, нам потребуется дополнительная константа С «∨», «&» и «¬» для реализации (*). Складывая (2n − 3 / (n − 3)) + (2n − 3 / (n − 3)) + С, получим как раз, что это ≲ 2n − 2 / n.
Оценка снизу
Оценка сложности ФАЛ
Оценка сверху
Оценка сложности самой сложной ФАЛ из класса
Оценка снизу
По заданной КС построить эквивалентную ей самокорректирующуюся КС.
Определение самокорректирующейся КС
(p, q)-самокорректирующейся КС называют КС, из которой всегда получается эквивалентная ей КС (реализующая те же формулы через все контакты) после p операций обрыва контакта (смена проводимости одного контакта с xσ на 0) и q операций замыкания контакта (смена проводимости одного контакта с xσ на 1).
Простейший способ построения
- Для защиты от одного разрыва каждый контакт заменяем на пару параллельных.
- Для защиты от n разрывов — на (n+1) дублирующих друг друга контактов.
- Для защиты от одного замыкания каждый контакт заменяем на пару последовательных.
- Для защиты от n замыканий — на (n+1) подряд идущих одинаковых контактов.
Итого, для (p, q)-самокорректирующей схемы мы каждый из контактов заменяем на последовательность из (q + 1) блоков, каждый из которых — параллельный пучок из (p + 1) контакта.
Пример
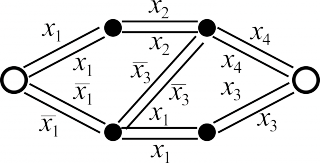
| Исходная контактная схема | Контактная схема, исправляющая один разрыв |
|---|---|
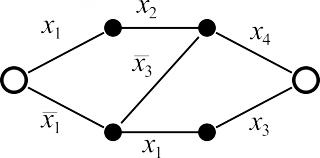
| 
|
| Контактная схема, исправляющая одно замыкание | Контактная схема, исправляющая один разрыв и одно замыкание |
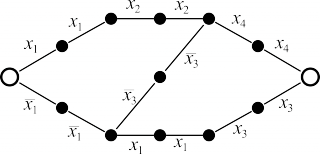
| 
|
Способы с оптимизацией числа дуг самокорректирующейся КС
Существуют способы предварительной модификации схемы, после чего к контактам нетронутой части применяется описанный выше алгоритм.
Для исправления одного замыкания
- Выделяем цикл из одинаковых контактов, вводим новую вершину и делаем ее центром звезды, на которую заменяем найденный цикл.
- Все контакты, не вошедшие ни в 1 цикл удваиваем последовательно.
- Данная конфигурация устойчива к одному замыканию, т.к. между любыми исходными узлами появляется не 1, а 2 контакта.
Для исправления одного обрыва цепи
- Выделяем звезду из одинаковых контактов, удаляем все кантакты звезды и соединяем все контакты циклом.
- Все контакты, не вошедшие ни в 1 звезду удваиваем параллельно.
- Данная конфигурация устойчива к одному обрыву, т.к. между любыми 2 узлами появляется не 1, а 2 пути.


