ВПнМ, 02 лекция (от 15 февраля)
Материал из eSyr's wiki.
Оригинальная презентация: http://savenkov.lvk.cs.msu.su/mc/lect2.pdf
Диктофонная запись: http://esyr.org/lections/audio/verification_2008_summer/verification_08_02_15.ogg
Можно либо изначально построить модель, либо в процессе разработки.
На первом этапе выделяем из требований классы свойств, и по описанию системы и классам св-в строим модель. после этого описываем конкретные свойства, которые проверяем в процессе верификации. Подаём модель и св-ва на вход верификатора и он проверяет. Дальше может быть несколько вариантов:
- Свойство выполняется. Если модель корректна, то программа корректна.
- Верификация не останавливается тогда, когда мы этого хотим. Это означает, что слишком сложная модель. Надо останавливать процесс вериф. и модернизировать модель
- Свойство не выполняется. Мы получаем контрпример, локализуем ошибку. Какая может быть ошибка?
- Неправильно описано свойство. Меняется свойство, повторная верификация
- Построили некорректную модель. По контрпримеру св-во нарушается в модели. Смотрим, где в описании оно нарушается и не находим. Неправильная модель
- Ошибка есть в описании. Исправляем программу
Верификация автоматизирована, но автоматизирован только сам процесс и частично построение модели. Участие человека довольно велико:построение модели, анализ результатов верификатора.
Содержание |
Построение модели
Модель нельзя построить без свойств, которым она должна удовлетворять.
Примеры классов свойств:
- Отсутствие тупика
- Отсутствует удушения
- Не срабатывают ассерты
- Зависящие от приложения
- Общий случай удушения
У нас есть система, строим более простую модель, на ней проверяем свойства. Причин строить модели две:
- Программа, написанная на инженерном ЯП, она предназначена для того, чтобы данные обрабатывать
- Абстракция от лишних осстояний
Мы хотим уменьшить пространство состояний. Что же такое состояний программы?
- Состояние программы --- какой оператор выполняется, что записано в память (не только переменные, но и любые ресурсы, с которыми работает программа).
Необходимо отметить, что если мы говорим про отдельные программы, то не так просто сказать, что такое состояние. Поэтому, когда мы говорим о состоянии программы, мы прибегаем к абстракции. Состояние атомов, из которых создан компьютер, нам неинтересно, нужно провести грань. Состояние всегда связано с моделью программы.
Есть три переменных и 7 операторов --- 7*2^96 состояния.
При этом, не все эти состояния по ходу порграммы достижимы. Число достижимых сост. меньше, чем потенциальных, и нужно понимать, что просто смотря, анализируя текст программы, мы не можем оценить достиж. сост, поскольку эта задача алгоритмически неразрешима.
второе число --- 6 * 3 * 2^64
Первая задача, которую мы получим по курсу --- будет прислан текст программы на С, и нужно будет оценить число потенциальных и дост. состояний, оценка должна быть обоснованная. По этому поводу лектор просит до след. среды написать на адрес model-checking@cs.msu.su, ФИО и группу и попросить дать порграмму. Если есть старосты групп, лектор просит прислать список групп
Прежде чем говорить о моделировании, нужно поговорить о модели программ. Если говорить о языке С, то в качестве примера рассмотрим программу, подсчитывающую количество строк. У этой программы может быть очень большое число состояний, посмотрим, как её можно упростить:
- Неважны имя файла
- Отладочный вывод
- Введём перечислимый тип
- Сделаем замену в теле функции --- ввести два предиката, заменяющие ветвление по содерж. файла
- Дальше хорошо бы абстрагироваться от файла и системных вызовов --- вводим абстрактные перем. и введём перем-сост. файла
- Можно абстрагироваться от потока управления
В результате увидим, что файл не закрываем.
Модель --- упрощённое описание реальности. С явлением может быть связано несколько моделей, и каждая может отражать своё свойство. У дома может быть много разных схем,если все свалить в одну, то в ней будет трудно разобраться, поэтому они разделены. Кроме того, электрику план водоснабжения может не сильно помочь, то есть модель должна быть адекватна.
Соответственно, модель должна быть простой, корректной, адекватной
С другой стороны, можно сделать слишком сильную абстракцию, которая не сильно поможет.
Процесс построения модели
- Необх. формализовать требования. Требования бывают формализуемые, бывают неформализуемые, бывают формализуемые, но не в этой области. Например, требование, чтобы самолёт летел и не падал --- требование формализуемое. А требование в стартапе рентабельность была выше 30% --- требование формализуемое, но не в модели программы. Можно формализовать требования удобства --- ввести сферического пользователя в вакуусе и даже проверить что-то на полученной модели, но ценность поддобного не высока.
- Далее необходимо выбрать язык моделирования. Как правило, программы написаны на инж языках, на которых удобно программировать и которые удобно компилировать. Требование удобства моделирования не на первом плане. Чем проще программистам, тем сложнее при моделировании
- Абстракция системы до модели. Обычно строят модель более простую, но из соображ. непротиворечивости будем ссылаться на прост. сост. исх. системы, и модели.
Рассмотрим пример программ consumer/producer
Рассм. св-ва, которые выполняются для producer:
- Отправка сообщ. выполняется после того, как иниц. очередь
- Если поток упр. попадает в ошибку, то отправка/получение не вызываются
- Ни в одном вычислении не вызывается два получения сообщ. без отправки сообщ. между ними
Проверим первое свойство.
Весь выделенные серым код не влияет на проверяемые св-ва. В результате можно ввести оператор pass(), оставить только вызовы. В результате получим, что св-во выполняется.
Проверим второе свойство. Для модели важно не нарушить поток выполнения и вызовы. Оно не выполняется.
Эта же модель подходит для свойства 3.
При этом, если мы немного по-другому сформулируем свойство корректности (всегда ли верно, что после ошибки не будет посылки), тогда при отсутствии send модели модель будет малоадекватна.
Для каждой программы можно построить такую модель ... , но мало свойств, которые можно проверить на такой модели.
Строго говоря
Сейчас будут введены те же понятия, но более строго.
У нас есть система в виде программы. Этой системе соответствует система переходов, в которй мы можем наблюдать набор трасс. Если система переходов очень большая, что мы строим модель, которая должна быть корректна.
Из того, что модель адекватна свойствам, мы заключим, что св-ва выполняются... Далее будут описаны упомянутые термины, а также отношение, между трассами и системами переходов. Описание отношений между программами требует описания операционной семантики, это будет дальше как надстрока, ибо это усложнение.
Размеченные системы переходов (LTS)
Та структура, которая задаёт пространство нашей модели.
TS = <S, Act, 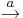 ,s_0, AP, L>
,s_0, AP, L>
У нас нет состояний, из которых никуда нельзя перейти, если есть что-то подобное, то там возникает петля с невидимым действием тау. Есть две школы: часть людей, что часть состояний (завершающие) должно быть нетотальными, другие говорят, что состояние завер. наблюдаемое и не происх. наблюдаемых действий, то там происходит ненабл. действие.
- S --- множество состояний
- Act --- множество действий, τ --- невидимое действие
- S × Act × S --- тотальное отн. переходов
- s_0 ∈ S --- начальное состояние
- AP --- множество атомарных высказываний
- L : ...
Пример размеченной системы переходов. Есть две переменных, с которыми что-то делают по условию.
Фактически пространство линейно.
Пример с двумя демонами.
На что здесь стоит обратить внимание. Здесь мы считаем, что сост. программы --- сост. сишных переменных, переход --- переход на си. Если мы рассм. программу на асм., то увидим, что это действие неатомарное, а так как программы работают параллельно, то сост. может быть больше.
Определяются потомки/предки сост, а также потомки/предки для класса
Детерминизм
Если у всех состояний нашей системы переходов есть только один потомок, то у нас система детерминированная. Иначе недетерминированная.
Недетрминизм --- это фича
Позволяет заменить условие недетерм. порядком вып., что позволяет строить модели.
Недетерминизм полезен для:
Мы наблюдае не за состоянием, а за изменением...
Достижимость
Чтобы посчитать достижимость, нужно отследить все фрагменты вычислений.
Трассы
Последовательность разметки состояний. Мы фокусируемся на наблюдаемых свойствах системы. Свойства описываются атомарными предикатами.
Свойства линейного времени (СЛВ)
Проверять мы можем свойства линейного времени. СЛВ определяет множество трасс, можно сказать, что оно принадлежит множеству трасс.
Система переходов удовлетворяет свойству линейного времени,если система трасс системы переходов включается в систему трасс свойства.
Абстракция
Формальное описание отношения абстракции. Трассу можно представить как интерпретацию: Множество натуральных чисел, отношение порядка и разметка кси, она для каждого порядкового номера говорит, что заданный в нём предикат истинный или ложен.
Рассмотрим две трассы, нам надо определить, что они связаны отношением абстракции. Эти две трассы имеют разные функции разметки (у одной может быть больше, у другой меньше), кроме того, состояниям могут соответствовать элементы трассы с разным номером. Будем говорить, что одна трасса является абстракцией другой, если множество наблюдаемых предикатов первой является подмножеством множества второй, сохраняются свойства частичного порядка и определено отображение и если какой-то предикат наблюдается в абстрактной трассе, то значение у него должно быть точно такое же, как и в детальной.
Пример:
мы рассмотрим свойства p и q, и есть предикаты p, q, r...
Возникает вопрос, как строить системы переходов, которые генерируют трассы, которые удовлетворяют отношению абстракции.
Пусть есть система, модель, свойство ЛВ. Если свойство выполняется на модели, то оно выполняется на системе. Мы тоже переформолируем это условие как ограничение на трассы. То есть, для любой трассы, которую может сгенерировать система, существует такая, которая может сгенерировать модель такую, что она является абстракцией системы. Если свойство выполняется на всех трассах модели, то, поскольку каждой трассе системы соответствует трасса модели, то свойство выполняется на трассах системы, и система корректна. Вопрос, как такое условие проверить, поскольку оно, вообщем в соотв. с этим опр., потребует большое количество ресурсов. Давайте сформулируем достаточное условие:
Пусть у нас есть система переходов исходной программы и модели. Чем они отл.: в модели прост. сост. меньше, алфавит действий меньше, в модели другое отн. переходов, другой алфавит предикатов, соотв. поменяется разметка. Мы поменяли всё. Если абстрактно поменяяем как угодно, то всё испортится. Наложим условие, как менять: множество состояний модели (первое условие в прямоугольнике лишнее), но вот алфавит предикатов модели совершенно точно включ. в алфавит системы, .... На отобрадение накл. ограничение, что нач. сост. системы должно отобр. в нач. сост. модели. Условие на сист. переходов: (Act' ∈ Act) каждому переходу из системы переходов системы должен соответствовать переход в модели.
Пока огр. таким опр.
Есть изьян в этом условии: можно построить такую модель, что нарушим одно из свойств.
Можно назвать это условие условно правильным.
Если кто-то хочет, может найти.
Если посмотреть расписание, то увидим разные практикумы. У СП два практикума. А у АСВК практикума Петровского нет.
Верификация программ на моделях
Календарь
| пт | пт | пт | пт | пт | |
Февраль
| 08 | 15 | 22 | 29 | |
Март
| 14 | 21 | 28 | ||
Апрель
| 04 | 11 | 18 |
Материалы по курсу
Список вопросов к экзамену | Примеры задач: 1 2 3 4 5 | Теормин


